Рівняння з однорідною функцією у правій частині

Функція називається однорідною відносно , якщо для будь якого дійсного .

Розглянемо рівняння вигляду

(1)

де однорідна функція. Його можна привести до вигляду

. (2)

Це рівняння приводиться до рівняння із відокремлюваними змінними. Для цього позначимо , де – нова невідома функція. Тоді . Після підстановки і в рівняння (2), одержимо звідки

(3)

Це рівняння із відокремлюваними змінними і 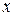. Після знаходження загального інтегралу рівняння (3) і заміни на , одержимо загальний інтеграл даного рівняння.