Лінійні рівняння першого порядку

Диференціальне рівняння називається лінійним рівнянням першого порядку, якщо воно лінійно (тобто першого степеня) відносно шуканої функції і її похідної .

З визначення випливає що таке рівняння має вигляд

. (1)

Якщо 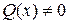, , то рівняння (1) називається лінійним неоднорідним, та якщо - лінійним однорідним.

Загальний розв’язок лінійного однорідного рівняння (2)

отримається відокремленням змінних:

або , де

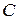- довільна стала.

Лінійне неоднорідне рівняння першого порядку можна інтегрувати методом Фур¢є. Згідно з цим методом невідому функцію y необхідно замінити добутком двох допоміжних функцій і v, тобто покласти . Тоді

,

і дане рівняння (1) прийме вигляд

. (3)

Користуючись тим, що одну з допоміжних функцій, наприклад v, можна вибрати довільно, підберемо її так, щоб вираз у квадратних дужках перетворився на нуль, тобто, візьмемо одне з частинних розв’язків рівняння (2). Наприклад,

(4)

Після підстановки (4) в (3) отримуємо рівняння відносно функції , яке є рівнянням із змінними, що розділяються. Нехай - загальний розв’язок цього рівняння. Тоді загальний розв’язок лінійного рівняння (1) дорівнює: .