 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение схем из функциональных элементов
|
|
Определение схемы из функциональных элементов распадается на две части. Вначале определяется один вспомогательный объект – сеть, а уже потом с его помощью определяется схема. Понятие сеть играет чисто вспомогательную роль и используется только для определения схемы из функциональных элементов. Сеть строится из полюсов и элементов.
○ – полюс (полюсы будем изображать маленькими кружочками)
1…n
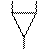 – элемент (каждый элемент имеет несколько входов, занумерованных числами 1, 2, …, и один выход; элементы будем изображать в виде треугольников с отростками, отростки сверху соответствуют входам элемента, а отросток снизу – его выходу).
– элемент (каждый элемент имеет несколько входов, занумерованных числами 1, 2, …, и один выход; элементы будем изображать в виде треугольников с отростками, отростки сверху соответствуют входам элемента, а отросток снизу – его выходу).
Определение логической сети:
I. Полюс есть логическая сеть, при этом он является ее единственной вершиной.
II. 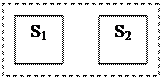 Если S1 и S2 – логические сети без общих вершин, то их объединение есть логическая сеть
Если S1 и S2 – логические сети без общих вершин, то их объединение есть логическая сеть  , вершинами которой являются вершины исходных логических сетей
, вершинами которой являются вершины исходных логических сетей  и
и 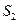 .
.
III. 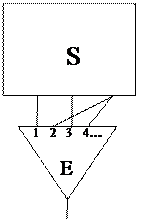 Если S – логическая сеть и E – элемент (входы и выход которого не являются вершинами S), то результат присоединения всех входов элемента E к некоторым вершинам S есть снова логическая сеть. При этом к одной вершине S могут присоединяться различные входы элемента Е, но каждый вход присоединяется только к одной вершине. Вершинами новой логической сети являются вершины S
Если S – логическая сеть и E – элемент (входы и выход которого не являются вершинами S), то результат присоединения всех входов элемента E к некоторым вершинам S есть снова логическая сеть. При этом к одной вершине S могут присоединяться различные входы элемента Е, но каждый вход присоединяется только к одной вершине. Вершинами новой логической сети являются вершины S
и выход элемента E.
Определение схемы. Схемой из функциональных элементов (СФЭ) называется логическая сеть, в которой:
1) Каждому полюсу приписана одна из переменных x1, …, xn, …, причем, разным полюсам – разные переменные, полюсы называются входами схемы;
2) Каждому элементу E с r входами поставлена в соответствие некоторая функция алгебры логики φЕ (y1,…,yr), существенно зависящая от r аргументов (при r=0 функция φЕ есть константа) и называемая функцией элемента E; элемент E с сопоставленной ему функцией φЕ называется функциональным элементом;
3) Вершины, которым приписано хотя бы одно из чисел, отмечены символом *. Эти вершины называются выходами схемы; l-м выходом из системы будем называть единственный выход, которому приписано число l.
Основные понятия и определения
Функции, реализуемые схемой, определяются следующим образом:
1) Каждому входу схемы сопоставляется функция, равная переменной, приписанной этому входу;
2) Пусть всем вершинам, к которым присоединены входы элемента Е схемы, уже сопоставлены функции. Тогда выходу этого элемента E сопоставляется функция φЕ (f(1),…,f(r)), где f(i) (1 ≤ i ≤ r) – функция, сопоставленная той вершине, с которой соединен i-й вход элемента Е.
В результате этого процесса каждой вершине схемы будет сопоставлена некоторая функция.
Определение. Схему с n входами, выходам которой приписаны числа 1,…, m, будем называть (n, m) – схемой.
Пример функции, реализуемой СФЭ. Пусть функция 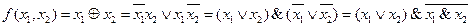 .
.
Тогда СФЭ, реализующие данную функцию, выглядят следующим образом: 

Определение. Если S – СФЭ, а L(S) – число элементов в схеме S, то L(S) называется сложностью схемы S.
Определение. Если функции всех элементов схемы S принадлежат множеству Б, то будем говорить, что схема S есть схема в базисе Б.
Замечание. В дальнейшем мы будем рассматривать схемы из функциональных элементов в базисе Б = (V,&,). Элементы, которым сопоставлены функции V, &,, будем называть соответственно дизьюнктором, коньюнктором и инвертором.
Рассмотримфункцию f(x1, …, xn) 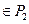 . Считается, что схема S, реализующая f, тем лучше, чем меньше ее сложность L(S). В этих условиях задача ставится так: для каждой функции f требуется найти реализующую ее схему S, на которой L(S) достигает минимума.
. Считается, что схема S, реализующая f, тем лучше, чем меньше ее сложность L(S). В этих условиях задача ставится так: для каждой функции f требуется найти реализующую ее схему S, на которой L(S) достигает минимума.
Обозначим этот минимум через L(f):
L(f) = 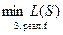 – min L(S) по всем схемам S, реализующим функцию f.
– min L(S) по всем схемам S, реализующим функцию f.
Вводим функцию L(n) = max L(f), где max берется по всем функциям от n аргументов.
L(n) = max L(f) – функция Шеннона.
f(x1, …, xn)ЄP2.
Другими словами, L(n) – минимальная сложность СФЭ, реализованной самой сложной функцией среди функций, зависящих от n переменных.
Основная задача синтеза: Найти такой метод синтеза схем, позволяющий для любой функции от n аргументов построить схему S, для которой L(S) близко к L(n), например, L(S)£L(n). Такой подход был предложен К.Э. Шенноном в 1949 г. при рассмотрении контактных схем и дан наилучший по порядку метод синтеза контактных схем.
Можно ли любую функцию алгебры логики реализовать схемой?
4.4. Возможность реализации любой функции
алгебры логики СФЭ
Теорема 1. Каждая функция f(x1, …, xn) Є P2 может быть реализована некоторой СФЭ S и притом L(S) ≤ n  2n+1, где n ³1.
2n+1, где n ³1.
Доказательство. При доказательстве этой теоремы используем метод синтеза, основанный на моделировании СДНФ.
Пусть 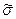 = (s1,…,sn). Рассмотрим конъюнкцию K
= (s1,…,sn). Рассмотрим конъюнкцию K 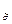 = x1s
= x1s 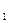 &…&xns
&…&xns 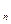 .
.
Схема для конъюнкции K 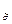 , приведенная на рисунке 1, состоит из n инверторов, присоединенных к входам схемы, и цепочки из n–1 конъюнкторов с n входами. Причем i-й вход цепочки присоединяется либо к i-му входу схемы, если si = 1, либо к выходу i-го инвертора, если si = 0, так как
, приведенная на рисунке 1, состоит из n инверторов, присоединенных к входам схемы, и цепочки из n–1 конъюнкторов с n входами. Причем i-й вход цепочки присоединяется либо к i-му входу схемы, если si = 1, либо к выходу i-го инвертора, если si = 0, так как
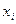 при si =1,
при si =1,
 xisi =
xisi =
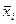 при si = 0.
при si = 0.

Рис. 1
Очевидно, что L(K 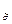 ) £ 2n – 1 ( 1 )
) £ 2n – 1 ( 1 )
Пусть f(x1, …, xn) – произвольная функция из P2 и
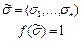 f(x1, …, xn) =
f(x1, …, xn) = 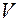
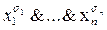 = K
= K 
 …
…  K
K 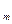 – ее СДНФ,
– ее СДНФ,
где 1 £ m £ 2 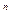 .
.
Тогда схема S для f строится из m схем для конъюнкций K 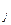 (1£ j £ m) и цепочки из m–1 дизъюнкторов (цепочка имеет m входов), объединяющей выходы схем для конъюнкций (рис. 2). Таким образом, учитывая (1),
(1£ j £ m) и цепочки из m–1 дизъюнкторов (цепочка имеет m входов), объединяющей выходы схем для конъюнкций (рис. 2). Таким образом, учитывая (1),
L(S) £ (2n–1)  m+m–1 = 2nm–m+m–1 = 2nm–1 < 2nm £ 2n
m+m–1 = 2nm–m+m–1 = 2nm–1 < 2nm £ 2n  2
2 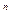 = n
= n  2
2 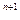
 L(S) £ n
L(S) £ n  2
2 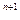 .
.

S:
Рис. 2
Мы доказали утверждение теоремы для любой функции, не равной тождественно 0.
Функция, тождественно равная 0, может быть реализована схемой, изображенной на рисунке 3, так как  &
& 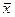 =0. Поэтому при n ³ 1
=0. Поэтому при n ³ 1
L(S) £ n  2
2 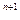 , так как L(1) = 2 < 1
, так как L(1) = 2 < 1  2
2 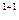 = 4. Теорема доказана полностью.
= 4. Теорема доказана полностью.

Рис. 3
Замечание. При доказательстве теоремы 1 использовался простейший метод синтеза, основанный на моделировании СДНФ.
Следствие. L(n) £ n  2n+1, где
2n+1, где 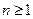 .
.
Дата публикования: 2014-10-20; Прочитано: 2865 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
