 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод синтеза
|
|
Схема S для функции f (x1, …, xn), заданной таблицей 1, строится на основе её представления (6) и состоит из 6 блоков (рис. 6):
1) Блок А реализует Q 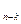 (x
(x 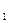 ,…,x
,…,x 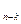 ), причем L(A)£(n-k)
), причем L(A)£(n-k)  2
2  .
.
2) Блок B реализует Q 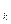 (x
(x 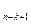 ,…,x
,…,x 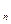 ), причем L(B) £k
), причем L(B) £k  2
2  .
.
3) Блок C реализует все различные функции f  (s1,…, s
(s1,…, s 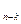 ,
,  ), тогда L(С) £p
), тогда L(С) £p  S
S  2
2  .
.
4) Блок D реализует все функции 
 =
=  , тогда L(D) £ p
, тогда L(D) £ p  2
2 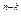 .
.
5) Блок G осуществляет умножение  , поэтому L(G)=2
, поэтому L(G)=2 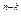
6) Наконец, блок F реализует функцию f(x1, …, xn) как дизъюнкцию функций, реализованных блоком G. L(F) £ 2 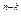 .
.
 S:
S:
Рис. 6
Итак, L(S) = L(A)+L(B)+L(C)+L(D)+L(G)+L(F)£(n-k)* 2  + k*2
+ k*2  +
+
+p*S*2  + p* 2
+ p* 2 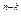 +2
+2  = (n-k+1)* 2
= (n-k+1)* 2  +k*2
+k*2  + p*S*2
+ p*S*2  + p* 2
+ p* 2 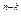 =
=
= (n-k+1)*2  +k*2
+k*2  +p*(2
+p*(2 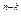 +S*2
+S*2  )£(n-k+1)*2
)£(n-k+1)*2  +k*2
+k*2  +(
+( +1)*(2
+1)*(2 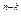 + S*2
+ S*2  ).
).
Положив k = [3 log n], s = [n-5 log n] получим L(S) £ 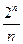 (1 + O(
(1 + O(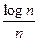 )) и L(n) £
)) и L(n) £ 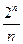 (1 + O(
(1 + O(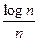 )). Теорема полностью доказана.
)). Теорема полностью доказана.
|
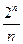 .
.
Теорема 5 (как следствие теорем 3 и 4). L(n) ~ 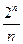 .
.
Замечание. Описанный метод синтеза в теореме 3 является асимптотически наилучшим.
Дата публикования: 2014-10-20; Прочитано: 808 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
