 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лемма о немонотонной функции
|
|
Лемма 4. Если 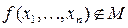 , то из неё путем подстановки констант 0 и 1 и функции
, то из неё путем подстановки констант 0 и 1 и функции  можно получить функцию
можно получить функцию 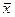 .
.
Доказательство: Пусть 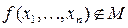 , тогда найдутся 2 набора
, тогда найдутся 2 набора 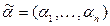 ,
, 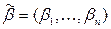 такие, что при
такие, что при 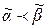
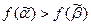 .
.
Так как 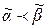 , то
, то 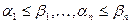 .
.
Пусть наборы 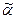 и
и 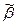 различаются в первых
различаются в первых 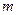 разрядах, где
разрядах, где  , то есть
, то есть
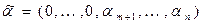
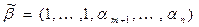
Рассмотрим функцию 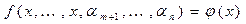 .
.
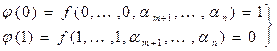 так как при
так как при 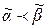
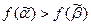 .
.
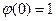 ,
, 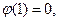 это значит,
это значит, 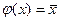 .
.
Лемма доказана.
3.20. Теорема о полноте в Р2
Теорема 7. Система функций 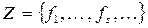 из
из 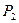 полна
полна  она целиком не содержится ни в одном из пяти замкнутых классов
она целиком не содержится ни в одном из пяти замкнутых классов 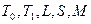 .
.
Доказательство: Необходимость 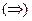 . Пусть
. Пусть 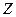 полна, то есть
полна, то есть 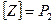 . Допустим, что
. Допустим, что 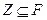 , где
, где  один из 5 перечисленных классов. Тогда в силу свойств замыкания и замкнутости
один из 5 перечисленных классов. Тогда в силу свойств замыкания и замкнутости  имеем
имеем 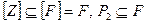 , противоречие.
, противоречие.
Достаточность 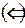 . Пусть
. Пусть 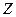 не содержится целиком ни в одном из пяти указанных классов, значит в
не содержится целиком ни в одном из пяти указанных классов, значит в 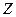
 функции
функции 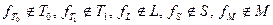 . Итак, из системы
. Итак, из системы 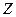 выделим подсистему
выделим подсистему 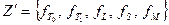 , которая также целиком не содержится ни в одном из пяти указанных классов. Будем считать, что все эти функции зависят от одних и тех же переменных
, которая также целиком не содержится ни в одном из пяти указанных классов. Будем считать, что все эти функции зависят от одних и тех же переменных 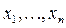 .
.
I. Построение констант 0 и 1 при помощи функций 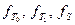 .
.
Рассмотрим 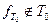 . Возможны два случая:
. Возможны два случая:
а) 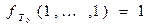 .
.
Пусть 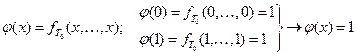 .
.
Возьмем 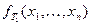 ;
; 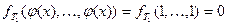 – вторая константа.
– вторая константа.
б) 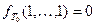 .
.
Пусть 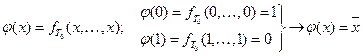 .
.
Рассмотрим 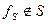 . Так как мы имеем
. Так как мы имеем  , то по лемме 3 мы можем получить константу
, то по лемме 3 мы можем получить константу 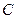 . Используя константу
. Используя константу 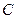 и
и  можем получить другую константу
можем получить другую константу 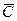 .
.
II. Построение функции  при помощи констант 0 и 1 и
при помощи констант 0 и 1 и 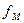 . Это следует из леммы 4.
. Это следует из леммы 4.
III. Построение 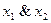 при помощи констант
при помощи констант 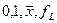 . Это осуществляется на основе лемм 1 и 2.
. Это осуществляется на основе лемм 1 и 2.
Таким образом, при помощи формул над 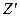 (а значит и над
(а значит и над 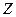 ) реализовали функции
) реализовали функции 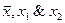 .
. 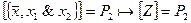 .
.
Теорема доказана полностью.
Из доказательства теоремы 7 следует
Следствие 8. Всякий замкнутый класс 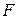 функций из
функций из 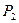 такой, что
такой, что 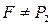 , содержится по крайней мере в одном из классов
, содержится по крайней мере в одном из классов 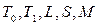 .
.
Дата публикования: 2014-10-20; Прочитано: 3530 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
