Предполные классы

Определение. Класс 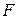функций из называется предполным, если , а .

Определение. Класс 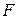функций из называется предполным, если 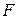неполный класс, а для функции класс – полный.

Из определения следует, что предполный класс замкнутый.

Следствие 9. В существуют только 5 предполных классов, а именно .

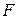Доказательство: Возьмем произвольный класс . По следствию 8 содержится в одном из пяти классов. Пусть .

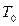а) , тогда , где , то есть 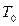– предполный по определению.

б) 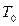, это значит, что , но 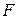не является предполным в , значит пункт б) отбрасывается из рассмотрения.

3.22. Возможность выделить из любой полной системы полную подсистему,
состоящую из не более чем 4-х функций

Теорема 8. Из всякой полной в системы функций можно выделить полную подсистему, содержащую не более четырех функций.

Доказательство: Согласно теореме 7 из системы функций можно выделить полную подсистему , содержащую не более 5 функций, то есть , .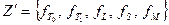

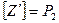Оказывается 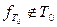, либо не самодвойственна (случай а пункта 1 в доказательстве теоремы 7), так как , либо не сохраняет единицу и не монотонна (случай б пункта 1 в доказательстве теоремы 7): . Поэтому полной будет либо система , либо система .

Теорема доказана.