 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод Шеннона
|
|
Описываемый ниже метод был предложен Шенноном для контактных схем в 1949 году. В последующие годы этот метод применялся другими авторами для других классов схем. Здесь метод излагается применительно к схемам из функциональных элементов.
|
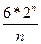 .
.
Доказательство. Напомним, что функция Шеннона L(n)=  , где L(f) =
, где L(f) = 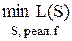 , а L(S) – сложность схемы S, реализующей булеву функцию f (x1, …, xn).
, а L(S) – сложность схемы S, реализующей булеву функцию f (x1, …, xn).
Разложим функцию f(x1, …, xn) по n-k переменным:
f(x1, …, xn) = 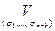
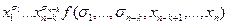 . (4)
. (4)
Схема S для функции f строится из трех блоков (подсхем) (рис. 5):
S: 
1) блока, реализующего Q 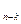 (x
(x 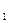 ,…,x
,…,x 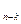 );
);
2) блока, реализующего систему V 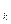 (x
(x 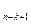 ,…,x
,…,x 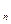 ) всех 2
) всех 2 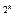 функций от переменных x
функций от переменных x 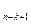 ,…,x
,…,x 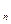 ;
;
3) блока, осуществляющего соединение первых двух блоков в соответствии с (4).
Заметим, что два первых блока не зависят от реализуемой функции f, а зависят только от разбиения аргументов функции f на два подмножества: {x 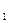 ,…,x
,…,x 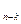 } и {x
} и {x 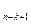 ,…,x
,…,x 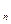 }.
}.
В третьем блоке на каждый член разложения (4) приходится не более одного конъюнктора и не более одного дизъюнктора.
Таким образом,
L(S) £ L(Q 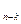 ) + L(V
) + L(V 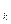 ) + 2
) + 2  2
2 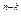 . (5)
. (5)
|
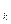 ) £ k
) £ k  2
2 
 2
2 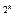 , согласно лемме L(Q
, согласно лемме L(Q 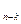 )~2
)~2 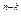 , тогда L(S) < 3
, тогда L(S) < 3  2
2 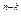 + k
+ k  2
2 
 2
2 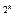 .
.
Положим (при достаточно больших n): k = [log(n – 3 log n)].
Тогда log(n – 3 log n)-1< k £ log (n – 3 log n) 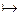 log(n – 3 log n) – log 2 < log 2
log(n – 3 log n) – log 2 < log 2 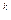 £ log(n – 3 log n)
£ log(n – 3 log n) 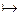
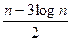 < 2
< 2 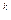 £ n – 3 log n,
£ n – 3 log n,
2 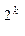 £ 2
£ 2 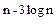 =
= 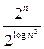 =
= 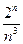 .
.
|
 2
2 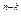 + k
+ k  2
2 
 2
2 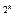 <
< 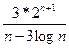 +
+ 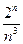 2n log n <
2n log n < 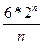 , так как
, так как 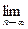
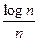 = 0.
= 0.
|
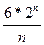 . Теорема полностью доказана.
. Теорема полностью доказана.
4.7. Асимптотически наилучший метод
(метод О.Б. Лупанова)
Асимптотически наилучший метод синтеза схем предложен О.Б. Лупановым в 1958 г.
Теорема 3. L(n) £ 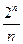 (1 + O(
(1 + O(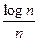 )).
)).
Доказательство теоремы строится из двух частей.
Дата публикования: 2014-10-20; Прочитано: 1294 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
