Представление о результатах Поста

Определение. Система функций называется базисом в замкнутом классе 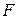, если , а .

Другими словами, базис класса есть его минимальная полная подсистема.

Пример: 1) - базис в .

2) - базис в .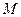

В 1921 г. появилось краткое сообщение о крупном исследовании в , выполненном известным американским математиком Э. Постом. Однако только через 20 лет, в 1941 г. автору удалось оформить этот труд в виде монографии «Two-valued iterative system». Монография написана на языке отношений и занимает очень большой объем. Основным результатом этой работы является построение всех замкнутых классов в . Формально основные результаты Поста можно сформулировать в виде следующих теорем:

Теорема 9. Каждый замкнутый класс из имеет конечный базис.

Теорема 10. Мощность множества замкнутых классов в счетна.

Хотя вторая из этих теорем логически следует из первой, тем не менее в доказательстве Поста сначала устанавливается второй факт, а затем – первый.

Заметим, более современное изложение результатов Поста имеется в книге «Функции алгебры логики и классы Поста» (см. дополнительную литературу [1] к разделу 3). Книга изложена на языке функций и занимает всего 120 страниц.