 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Простейшие методы синтеза
|
|
1. Метод синтеза, основанный на моделировании СДНФ.
2. Модификация предыдущего метода, заключающаяся в совместной реализации конъюнкций.
Метод синтеза, основанный на моделировании СДНФ, наглядно описали при доказательстве теоремы 1 (рис. 2).
Далее опишем следующий метод, заключающийся в совместной реализации конъюнкций (лемма).
Обозначим через L  (F/G) минимальную сложность схемы (в базисе Б), которую надо присоединить к схеме, реализующей функцию G, чтобы полученная схема реализовала функцию F. Очевидно, что
(F/G) минимальную сложность схемы (в базисе Б), которую надо присоединить к схеме, реализующей функцию G, чтобы полученная схема реализовала функцию F. Очевидно, что
L  (F)
(F)  L
L  (G)+ L
(G)+ L  (F/G). (2)
(F/G). (2)
В нашем случае Б = (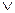 , &, -).
, &, -).
Пусть Qn (x1,…,xn) = {x1s1&…&xnsn} – система всех 2n конъюнкций от переменных x1,…,xn.
Лемма. L(Qn) ~ 2n (сложность реализаций всех конъюнкций от n переменных).
Доказательство. Конъюнкцию x1s1&…&xnsn можно разбить на 2 части:
x1s1&…&xmsm и xm+1sm+1&…&xnsn.
Очевидно, что каждая конъюнкция x1s1&…&xnsn из Q 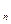 (x
(x 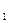 ,…,x
,…,x 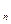 ) является конъюнкцией двух конъюнкций: x1s1&…&xmsm из Q
) является конъюнкцией двух конъюнкций: x1s1&…&xmsm из Q 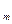 (x
(x 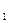 ,…,x
,…,x 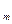 ) и xm+1sm+1&…&xnsn из Qn-m (xm+1,…,xn).
) и xm+1sm+1&…&xnsn из Qn-m (xm+1,…,xn).
Поэтому (согласно рис. 4)
L(Q 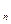 / Q
/ Q 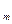 , Q
, Q  )£2
)£2 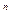 . (3)
. (3)

Рис. 4
Из (1) следует, что
L(Q 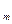 )£(2m-1)*2
)£(2m-1)*2  £m*2
£m*2 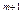 ,
,
L(Q  )£[2(n-m)-1]*2
)£[2(n-m)-1]*2  £(n-m)*2
£(n-m)*2  .
.
Поэтому, учитывая (2) и (3), имеем L(Q 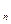 )£ L(Q
)£ L(Q 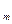 )+ L(Q
)+ L(Q  )+ L(Q
)+ L(Q 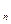 / Q
/ Q 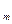 , Q
, Q  )£ m*2
)£ m*2 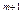 +(n-m)*2
+(n-m)*2  +2
+2 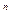 .
.
Положим теперь m = [ 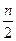 ]. Тогда m*2
]. Тогда m*2 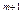 £
£ 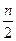 *2
*2  ,
,
|
 £(
£(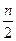 +1)*2
+1)*2  . Значит, L(Q
. Значит, L(Q 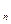 )
)  < 2n.
< 2n.
С другой стороны, очевидно, что при n ³ 2 L(Q 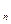 )³2
)³2 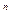 , так как каждая конъюнкция реализуется на выходе некоторого элемента.
, так как каждая конъюнкция реализуется на выходе некоторого элемента.
Таким образом, L(Q 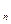 )~2n. Лемма доказана.
)~2n. Лемма доказана.
|
|
 , имеем: L(f)
, имеем: L(f)  L(Q
L(Q 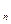 ) + 2
) + 2 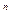 , так как L(Q
, так как L(Q 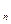 )~2
)~2 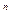 , то L(f) < 2*2
, то L(f) < 2*2 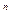 . Значит, L(n) < 2*2
. Значит, L(n) < 2*2 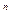 .
.
Дата публикования: 2014-10-20; Прочитано: 796 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
