Функция f(x1, …, xn) может быть задана таблицей 1, в которой значение f(s1,…,sn) функции f на наборе (s1,…, s 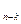 ,s
,s  ,…,sn) помещается на пересечении столбца, соответствующего (s1,…,sn-k), и строки, соответствующей (s
,…,sn) помещается на пересечении столбца, соответствующего (s1,…,sn-k), и строки, соответствующей (s  ,…,sn):
,…,sn):
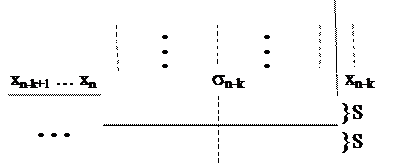

| | | | |
| | | f(s1, …, sn-k, sn-k+1, …, sn)
,
| |
| | | |
| |
Разобьем строки таблицы 1 на полосы A 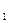 ,…,A
,…,A  по S строк в полосе (последняя полоса может содержать меньшее число строк). Ясно, что
по S строк в полосе (последняя полоса может содержать меньшее число строк). Ясно, что
p£  +1.
+1.
Пусть f  – функция, совпадающая с f на полюсе A
– функция, совпадающая с f на полюсе A  и равная 0 вне этой полосы. Очевидно, что f(x1, …, xn) =
и равная 0 вне этой полосы. Очевидно, что f(x1, …, xn) =  f
f  (x1, …, xn) =
(x1, …, xn) =


 =
=



 . (6)
. (6)
Заметим, что в (6) каждая из функций f  (s1,…, s
(s1,…, s 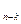 ,
,  ) задается одним столбцом таблицы для функции f
) задается одним столбцом таблицы для функции f  и поэтому принимает значение 1 не более чем на S наборах, так как функция f
и поэтому принимает значение 1 не более чем на S наборах, так как функция f  совпадает с функцией f только на полосе A
совпадает с функцией f только на полосе A  и равна нулю вне этой полосы. Таким образом, число различных функций f
и равна нулю вне этой полосы. Таким образом, число различных функций f  (s1,…,s
(s1,…,s 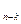 ,
,  ) (при фиксированном i) не превосходит 2
) (при фиксированном i) не превосходит 2  .
.

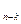 ,s
,s  ,…,sn) помещается на пересечении столбца, соответствующего (s1,…,sn-k), и строки, соответствующей (s
,…,sn) помещается на пересечении столбца, соответствующего (s1,…,sn-k), и строки, соответствующей (s  ,…,sn):
,…,sn):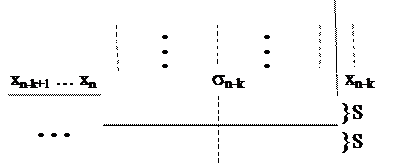


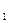 ,…,A
,…,A  по S строк в полосе (последняя полоса может содержать меньшее число строк). Ясно, что
по S строк в полосе (последняя полоса может содержать меньшее число строк). Ясно, что +1.
+1. – функция, совпадающая с f на полюсе A
– функция, совпадающая с f на полюсе A  и равная 0 вне этой полосы. Очевидно, что f(x1, …, xn) =
и равная 0 вне этой полосы. Очевидно, что f(x1, …, xn) =  f
f  (x1, …, xn) =
(x1, …, xn) =

 =
=


 . (6)
. (6) (s1,…, s
(s1,…, s 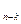 ,
,  ) задается одним столбцом таблицы для функции f
) задается одним столбцом таблицы для функции f  и поэтому принимает значение 1 не более чем на S наборах, так как функция f
и поэтому принимает значение 1 не более чем на S наборах, так как функция f  совпадает с функцией f только на полосе A
совпадает с функцией f только на полосе A  и равна нулю вне этой полосы. Таким образом, число различных функций f
и равна нулю вне этой полосы. Таким образом, число различных функций f  (s1,…,s
(s1,…,s 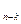 ,
,  ) (при фиксированном i) не превосходит 2
) (при фиксированном i) не превосходит 2  .
.