 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Самодвойственные функции, их свойства
|
|
Определение. Функция 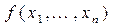 , для которой выполняется равенство
, для которой выполняется равенство 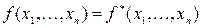 , называется самодвойственной.
, называется самодвойственной.
Класс всех самодвойственных функций из 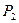 обозначим через
обозначим через  .
.
Очевидно, 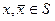 . Покажем, что
. Покажем, что
 .
.
Действительно, согласно принципу двойственности,
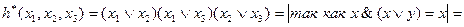
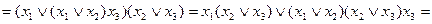
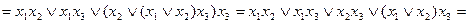
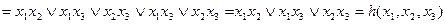 .
.
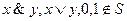 .
.
Из определения следует, что 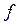 самодвойственная функция
самодвойственная функция 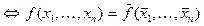 , то есть на противоположных наборах
, то есть на противоположных наборах 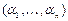 и
и 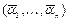 самодвойственная функция принимает противоположные значения. Отсюда следует, что самодвойственная функция полностью определяется своими значениями на первой половине строк её табличного представления, то есть
самодвойственная функция принимает противоположные значения. Отсюда следует, что самодвойственная функция полностью определяется своими значениями на первой половине строк её табличного представления, то есть 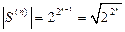 .
.
Утверждение 5. Класс  замкнут.
замкнут.
Доказательство: Так как 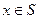 , то достаточно показать, что функция
, то достаточно показать, что функция 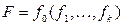 является самодвойственной, если функции
является самодвойственной, если функции 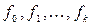 самодвойственны.
самодвойственны.
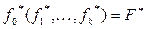 по утверждению 4. Так как
по утверждению 4. Так как 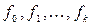 самодвойственны, то
самодвойственны, то 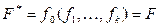 .
.
Дата публикования: 2014-10-20; Прочитано: 1237 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
