Монотонные функции, их свойства

Рассмотрим два набора , .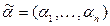

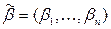Определение. Для двух наборов 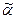и 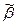выполнено отношение предшествования 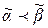, если .

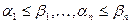Пример: , .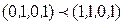

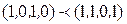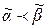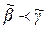Очевидно, если и , то 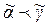. Отметим, что не любые пары наборов находятся в отношении предшествования, поэтому множество всех наборов длины 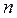по отношению к операции предшествования является частично упорядоченным.

Определение. Функция 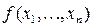называется монотонной, если для любых двух наборов 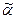и 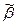, таких, что 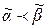, имеет место неравенство .

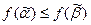Обозначим через 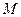множество всех монотонных функций из .

, .

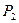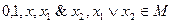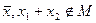Утверждение 6. Класс 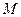замкнут.

Доказательство: Так как 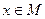, то для установления замкнутости класса 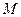достаточно показать, что функция 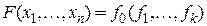является монотонной, если 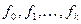монотонны.

Пусть 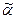и 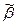– два набора длины 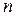значений переменных 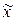, причем .

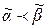Надо показать, что .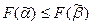

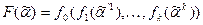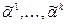, где – поднаборы .

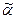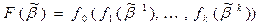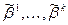, где – поднаборы .

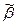Так как 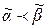, то .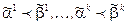

А поскольку 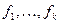монотонны, то .

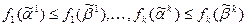Тогда .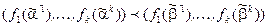

Так как 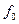монотонна, то .

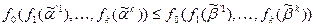Отсюда следует, что 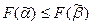, а это значит, 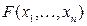монотонна.