Лемма о несамодвойственной функции

Лемма 3. Если , то из неё путем подстановки функций и 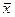можно получить константу.

Доказательство: Так как , то найдется набор такой, что .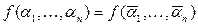

Рассмотрим функции .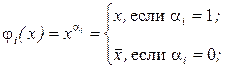

Положим .

Мы имеем

то есть

Так как 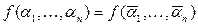, то , значит – константа.

Лемма доказана.

Пример: Пусть дана функция такая, что .

Рассмотрим функцию

– константа.