Принцип двойственности

Определение. Функция 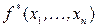, равная , называется двойственной функцией к функции .

Легко видеть, что среди функций

функция двойственна ,

двойственна ,

двойственна ,

двойственна ,

двойственна ,

двойственна .

Действительно, , .

Из определения двойственности вытекает, что , то есть функция является двойственной к (свойство взаимности).

Утверждение 4. Пусть , тогда .

Доказательство:

.

Из утверждения 4 вытекает принцип двойственности:

Если формула , построенная над множеством , реализует функцию , то формула , построенная заменой на для , реализует функцию , двойственную той, которую реализует формула .

Пример: Для формул над множеством принцип двойственности может быть сформулирован так: для получения формулы над , двойственной к формуле над , нужно в формуле над всюду заменить на , на , на , на .