 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Замыкание. Свойства операции замыкания
|
|
Замкнутые классы
С понятием полноты тесно связано понятие замыкания и замкнутого класса.
Определение. Пусть 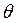 – некоторое подмножество функций из
– некоторое подмножество функций из  . Замыканием
. Замыканием 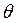 называется множество всех булевых функций, представимых в виде формул через функции множества
называется множество всех булевых функций, представимых в виде формул через функции множества 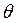 . Замыкание множества
. Замыкание множества 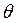 обозначается через
обозначается через 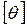 .
.
Отметим некоторые свойства замыкания:
1) 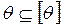 ;
;
2) 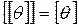 ;
;
3) если 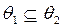 , то
, то 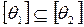 ;
;
4) если мы рассмотрим 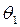 и
и 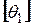 ,
, 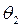 и
и 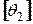 , то
, то 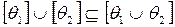 .
.
Определение. Класс (множество) 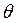 называется замкнутым, если
называется замкнутым, если 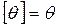 .
.
Пример:
1) Класс 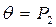 является замкнутым классом.
является замкнутым классом.
2) 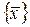 – незамкнутый класс, так как
– незамкнутый класс, так как 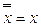 , а
, а 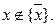

3) 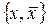 – незамкнутый класс, так как подстановкой других переменных мы можем получить из функции
– незамкнутый класс, так как подстановкой других переменных мы можем получить из функции 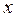 функцию
функцию 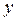 , а
, а 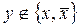 .
.
Замечание. В терминах замыкания и замкнутого класса можно дать другое определение полноты: 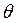 – полная система, если
– полная система, если 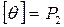 .
.
3.13. Классы 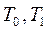 и их свойства
и их свойства
Определение. 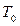 – класс всех булевых функций
– класс всех булевых функций 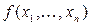 , сохраняющих константу 0, то есть функций, для которых выполнено
, сохраняющих константу 0, то есть функций, для которых выполнено 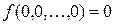 .
.
1) 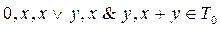 , но
, но 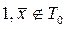 .
.
2) 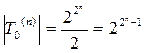 .
.
Утверждение 2. 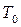 – замкнутый класс.
– замкнутый класс.
Доказательство: Так как 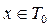 , рассмотрим суперпозицию
, рассмотрим суперпозицию
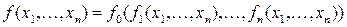 ,
,
где 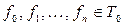 . Тогда
. Тогда
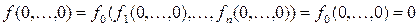 .
.
Это означает, что любая суперпозиция функций из класса 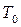 сохраняет константу 0, т.е. класс
сохраняет константу 0, т.е. класс 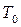 замкнут.
замкнут.
Определение. 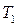 – класс всех булевых функций
– класс всех булевых функций  , сохраняющих константу 1, то есть функций, для которых выполнено
, сохраняющих константу 1, то есть функций, для которых выполнено 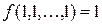 .
.
1) 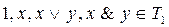 , но
, но 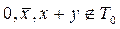 .
.
2) 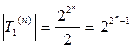 .
.
Утверждение 3. 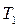 – замкнутый класс.
– замкнутый класс.
Доказательство: Так как  , то достаточно показать, что функция
, то достаточно показать, что функция 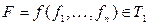 , если
, если 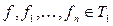 . Действительно,
. Действительно, 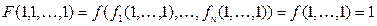 .
.
Дата публикования: 2014-10-20; Прочитано: 3154 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
