Формула решета

Пусть r – четно, q – нечетно, тогда

,

.

Теорема 3. (формула решета).

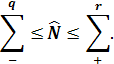
для любых r, q, где r – четно, q – нечетно.

Доказательство: Идея доказательства аналогична доказательству формулы (2).

1. Докажем неравенство

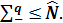(3)

Для доказательства неравенства (3) достаточно показать, что для любого элемента x измножества Е вклад его в левую часть неравенства (3) меньше, чем в правую.

1) Пусть элемент x из множества Е не обладает никакими свойствами множества Р. Тогда в (3) элемент x слева и справа учитывается 1 раз.

2) Пусть элемент x из множества Е обладает свойствамиp₁,...,p_к, где

k = 1,…,n. Возможны два случая:

а) q>k – получаем одинаковый вклад в (3): 0=0.

б) q . В этом случае слева получаем вклад в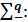

.

Итак, в левой части неравенства (3) элемент x дает отрицательный вклад, а в правой части вклад равен 0.

Таким образом, мы доказали, что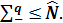

2. Неравенство доказывается аналогично.