 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Булевы функции
|
|
Рассмотрим 2-х элементное множество  , далее n-ю декартовую степень множества
, далее n-ю декартовую степень множества 
 , элементами этого множества являются наборы:
, элементами этого множества являются наборы: 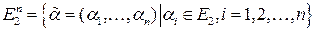 .
.
Определение. Булевой функцией называется функция, у которой как переменные, так и сама функция принимают значения из  .
.
Таким образом, булева функция  отображает
отображает  . Функцию
. Функцию  удобнее всего задать в виде таблицы:
удобнее всего задать в виде таблицы:

| 
|
| 0 0 … 0 0 0 … 1 ....... 1 1 … 0 1 1 … 1 | 
 .......
.......
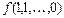

|
Обозначим через  множество всех булевых функций (или
множество всех булевых функций (или  – двухзначная логика), через
– двухзначная логика), через  – множество всех функций из
– множество всех функций из 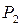 , зависящих от n переменных.
, зависящих от n переменных.
Утверждение 1. |  |=
|=  .
.
Доказательство: Это соотношение непосредственно следует из табличного построения функций.
Наборов значений переменных длины  из нулей и единиц в таблице –
из нулей и единиц в таблице –  . Для
. Для  набора функция принимает значение 0 или 1. Поэтому всего количество функций –
набора функция принимает значение 0 или 1. Поэтому всего количество функций – 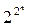 .
.
Примеры некоторых элементарных булевых функций:
1) Функции от одной переменной:
| x | 0(x) | 1(x) | x | 
|
2) Функции от двух переменных:

| 
| 
| 
| 
| 
| 
| 
|
| 0 0 0 1 1 0 1 1 |
Приведем названия этих функций.
 – тождественная функция.
– тождественная функция.
 = x – отрицание
= x – отрицание  , читается «не
, читается «не  » или «неверно, что
» или «неверно, что  ».
».
 – конъюнкция
– конъюнкция  и
и  , читается «
, читается « и
и  ».
».
 – дизъюнкция
– дизъюнкция  и
и  , читается «
, читается « или
или  ».
».
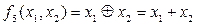 – сумма по модулю 2
– сумма по модулю 2  и
и  , читается
, читается
« плюс
плюс  ».
».
 – импликация
– импликация  и
и  , читается «если
, читается «если  , то
, то  ».
».
 – штрих Шеффера
– штрих Шеффера  и
и  , читается «не
, читается «не  или не
или не  ».
».
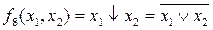 – стрелка Пирса
– стрелка Пирса  и
и  , читается
, читается
«не  и не
и не  ».
».
 – эквиваленция
– эквиваленция  и
и  , читается
, читается
« эквивалентно
эквивалентно  ».
».
Определение. Рассмотрим функцию  .
.
1. Переменная  , называется существенной для функции
, называется существенной для функции  , если
, если  такие значения
такие значения  , что
, что  .
.
2. Переменная 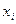 называется несущественной или фиктивной для функции
называется несущественной или фиктивной для функции  , если она не является существенной.
, если она не является существенной.
Примеры:
1) В функциях  переменная
переменная  фиктивная.
фиктивная.
2) В функциях  переменная
переменная  существенная.
существенная.
3) Пусть нам дана функция f (x 1, x 2) =  .
.
а) проверим  на существенность, пусть
на существенность, пусть  , тогда
, тогда  , тогда по определению
, тогда по определению  – существенная переменная;
– существенная переменная;
б) проверим  на существенность, пусть
на существенность, пусть  , тогда
, тогда  ; пусть
; пусть  , тогда
, тогда  , значит,
, значит,  по определению существенная.
по определению существенная.
Таким образом, в функции f (x 1, x 2) =  обе переменные существенные.
обе переменные существенные.
4) В функциях  ,
,  ,
,  , x 1↓ x 2, x 1↔ x 2, x 1→ x 2 проверить переменные на существенность самостоятельно.
, x 1↓ x 2, x 1↔ x 2, x 1→ x 2 проверить переменные на существенность самостоятельно.
Определение. Две функции  и
и  называются равными
называются равными  , если они отличаются друг от друга только фиктивными переменными.
, если они отличаются друг от друга только фиктивными переменными.
Примеры:
1) 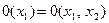 ;
;
2)  .
.
Замечание. В дальнейшем всюду функции рассматриваются с точностью до фиктивных переменных, т.е. если задана функция  , то задана и любая равная ей функция
, то задана и любая равная ей функция  .
.
Как сравнивать функции с разными переменными – рассматривать функции на наборах всех различных переменных, введя последние в данную функцию как фиктивные.
Пример:

| 
| 
|
| 0 0 0 1 1 0 1 1 |
 ,
,
 .
.
Из таблицы видно, что 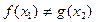 .
.
Дата публикования: 2014-10-20; Прочитано: 1144 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
