Принцип включения и исключения

Основная теорема, которую мы докажем, есть обобщение следующих очевидных формул:

1) ,

2) ,

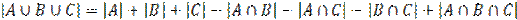которые справедливы для произвольных множеств А, В, С (их графическое изображение приведено ниже):

Принцип включения и исключения дает формула включения и исключения.

Пусть имеется множество Е = { x₁,..., x_N } элементов и множество P = { p₁,...,p_n } свойств. Будем считать, что любой элемент Є Е, где i = 1,...,N, может обладать любым набором свойств из множества P, а может и не обладать никаким свойством из множества P.

Через обозначим число элементов из множества Е, которые

обладают свойствами .Заметим, каждый из этих элементов может

обладать и другими свойствами.

Через обозначим число элементов из множества Е, которые обладают какими-нибудь k свойствами из множества P, где k = 1,…, n.

Положим W(0) = |E| = N.

Ставится задача: как, зная величины W(0), W(1), …, W(n), найти число элементов из множества Е, которые никаким свойством из множества P не обладают. Обозначим это число через 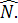Тогда

Теорема 2 (формула включения и исключения).

(2)

Доказательство: Для доказательства формулы (2) необходимо показать, что каждый элемент из множества Е учитывается одинаковое количество раз слева и справа формулы (2), т.е. любой элемент х ÎЕ дает одинаковый вклад как в левую, так и в правую часть формулы (2).

Возможны 2 случая.

Случай 1. Пусть элемент х из множества Е не обладает никакими свойствами множества P. Тогда слева он учитывается один раз. Cправа x будет учитываться в W(0) один раз, а больше учитываться не будет, так как W(1), …, W(n) учитывают элементы, обладающие каким-либо свойством. Мы получили равенство.

Случай 2. Пусть элемент х из множества Е обладает свойствами p_{1 ,...,} p_{k ,}где k=1,…, n. Тогда слева он дает вклад 0. Справа рассмотрим некоторое число s и определим входимость элемента x в W(s).

Возможны два варианта:

а) s>k – элемент x вклада в W(s) не дает, так как он обладает k свойствами;

б) s k – элемент x в W(1) дает вклад, равный 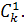,в W(2) - , в W(3) = ,…, W(k) = . Таким образом, вклад справа равен

1 – 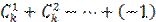^k = 0 в силу свойства 6 биномиальных коэффициентов.

В итоге мы получили равенство 0 = 0. Теорема доказана.

Пример 14. Из 100 студентов английский язык знают 28 студентов, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, все 3 языка знают 3 студента. Сколько студентов не знают ни одного из трех языков?

Решение: По формуле включения и исключения (2)

= 100 – (28 + 30 + 42) + (8 + 10 + 5) – 3 = 100 – 100 + 23 – 3 = 20. Итак, 20 студентов не знают ни одного из трех языков.