Различные комбинаторные соотношения

Правило суммы. Если есть конечные множества А и В, причем
A ∩ B = Ø, тогда |A U B| = |A| + |B| (число элементов в объединении множеств есть сумма чисел элементов в множествах).

Правило произведения. Пусть A´B = {(, )/ 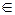A, 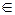B} – декартово произведение множеств A и B, тогда |A´B| = |A|·|B| (мощность множества АxВ есть произведение мощностей множеств А и В).

Пример 1. Пусть A = {1,2}, B = {a, b, c}. Тогда
A´B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}. |A´B| = |A|·|B| = 2·3 = 6.

Правило можно обобщить на n множеств: Пусть А₁,...,А_n – различные множества, тогда А₁´... ´А_n = {(α₁, α₂,…, α_n) | α₁ 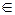А₁, α₂ 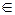А₂,…, α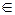_n А_n}
и |А₁´... ´А_n| = |А₁|•|А₂|•••|А_n|.

Пример 2. Найти число двоичных наборов длины n.

Решение: Пусть А₁ = {0,1}, …, А_n = {0,1}. Тогда

, где E₂ = {0,1}.

Пусть нам дано некоторое конечное множество X = {x₁, …,x_n}. Рассмотрим некоторое его подмножество { }. В дальнейшем такое подмножество назовем r-выборкой.

R-выборки бывают двух видов:

1. Если в r-выборке важен порядок элементов, тогда мы будем называть ее r-перестановкой из n элементов.

2. Если в r-выборке порядок элементов не важен, тогда будем называть ее r-сочетанием из n элементов.

В каждом из видов возможны 2 случая:

а) Допускается повторение элементов, тогда это r-перестановки с повторениями (или r-сочетания с повторениями).

b) Все элементы разные, тогда это r-перестановки без повторений (или r-сочетания без повторений).

Утверждение 1. Число r-перестановок с повторениями из n элементов П(n,r) = n^r.

Доказательство: Так как мы на каждое место можем поставить любой из n элементов, а таких мест r, значит всего возможностей по правилу произведения n^r. Действительно, А₁ = X,…,А_r = X, тогда .

Пример 3. X = {1,2,3}. Сколько двузначных чисел мы можем составить из элементов множества X?

Решение: Их всего n^r, где n = 3, r = 2. Тогда 3² = 9 чисел, а именно числа 11, 21, 31, 12, 22, 32, 13, 23, 33.

Утверждение 2. Число r-перестановок без повторений из n элементов , где .

Доказательство: , ; А₂ = Х₁, где , , …,

, где , 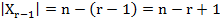. Другими словами, на первое место можно поставить n штук элементов, на второе – элементов и так далее, на последнее r-е место можно поставить
n – r + 1 элементов. Тогда по правилу произведения

_r | = .

Замечание. Очень часто r-перестановки без повторений из n элементов в литературе называют размещением из n элементов по r. Приняты следующие обозначения P(n,r) = A^r_n = (n)_r (число размещений из n элементов по r).

Пример 4. Х = {1,2,3}. Сколько двузначных чисел без повторяющихся цифр можно составить из элементов множества Х?

Решение: Их всего P(n,r) = n(n – 1)(n – 2)...(n – r + 1), где n = 3, r = 2. Тогда P(3,2) = 3·2 = 6 чисел (12, 21, 13, 31, 23, 32).

Следствие 1. Если в утверждении 2 r=n, то это перестановка из n элементов, и тогда .

Пример 5. X = {1,2,3}. Сколько трехзначных чисел без повторяющихся цифр можно составить из элементов множества Х?

Решение: их всего P_n = n!, где n = 3. Тогда P₃ = 3! = 1·2·3 = 6 чисел: 123, 213, 231, 321, 312, 132.

Формула Стирлинга: (~ – асимптотически равно).

Если , то .

Утверждение 3. Число r-сочетаний без повторений из n элементов .

Доказательство: Берем произвольную неупорядоченную выборку { 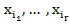} – r-элементов. Из этой одной неупорядоченной получаем r! упорядоченных. А так как всего неупорядоченных выборок , то – число упорядоченных выборок. Поскольку каждая упорядоченная выборка получена перестановкой элементов в неупорядоченной, то

.

Пример 6. X = {1,2,3}. Найти : 12, 13, 23 (неупорядоченные двузначные числа без повторяющихся цифр).

Пример 7. В чемпионате страны по футболу участвуют 18 команд, причем каждые две команды встречаются между собой 2 раза. Сколько матчей играется в течение сезона?

Решение: В первом круге состоится столько матчей, сколько существует двухэлементных подмножеств у множества, содержащего 18 элементов, т.е. их число равно = 153.

Во втором круге играется столько же матчей, поэтому в течение сезона состоится 306 встреч.

Числа , где r = 0,1,…,n называют биномиальными коэффициентами.

0! = 1 (по определению, для удобства).

2.3. Свойства биномиальных коэффициентов.
Биномиальная теорема. Полиномиальная теорема

1) – целое число.

2) : = , = → ().

3) : .

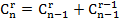4) Биномиальная теорема. . (1)

Доказательство: →

→ элемента;

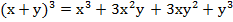→ элементов.

Надо узнать, какой коэффициент 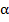при → → после перемножения получается различных комбинаций, но некоторые элементы повторяются. То есть коэффициент при равен числу
r-сочетаний x из всех n скобок, где , то есть . ■

5) Следствие 2. Если в формуле (1) x = y = 1, то

.

6) Следствие 3. Если в формуле (1) x = -1, y = 1, то

.

Пример 8. Найти число двоичных наборов длины n из 0 и 1, имеющих r единиц.

Решение: Всего двоичных наборов длины n из 0 и 1 – 2ⁿ, из них, имеющих r единиц, равно

= .

Пример 9. Для освещения зала может быть включена каждая из 10 ламп. Сколько существует различных способов освещения зала?

Решение: Очевидно столько, сколько существует подмножеств у десятиэлементного множества, т.е. . При этом учитывается и тот способ освещения, при котором ни одна лампа не горит.

Пример 10. Записать комплексное число в алгебраической форме.

Решение: По формуле (1) имеем

.

Значит, (2+i)⁶ = –117 + 44i.

7) a) Пусть (четное число), тогда .

b) Пусть (нечетное число),тогда

,

где [n/2] – целая часть числа n/2.

Доказательство:

a) Надо доказать, что , если , где r = 0, 1,…, – 1.

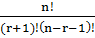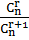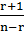= , = , = = < 1. Так как , то ; n – r ≥ r+1+1. Тогда (r+1)/(n-r) ≤(r+1)/((r+1)+1) <1.

Доказательство для b) аналогично.

Утверждение 4. Число r-сочетаний с повторениями из n элементов

.

Доказательство: Пусть {x₁,…, x_n} – наши элементы, из них выберем r элементов { } без учета порядка, но с повторением.

Пусть x₁ встречается α₁ раз,

x₂ встречается α₂ раза,

…

x_n встречается α_n раз,

где 0≤ α_i≤ r, 1≤ i≤ n; α₁ + α₂ +…+ α_n = r.

Число наших выборок равно числу решений нашего уравнения в целых положительных числах. Итак, выборка дает решение , и наоборот, решение дает выборку, то есть взаимнооднозначное соответствие между уравнением и выборками.

Пусть α₁,…,α_n – решение уравнения . Тогда выписываем α₁ единиц, затем 0, затем α₂ единиц, затем 0, и так далее:

0 0…0 .

В этом наборе единиц r штук, нулей (n – 1) штук.

По каждому решению уравнения получим наборы из 0 и 1 длиной r + n – 1.

Итак, каждый такой набор дает решение . Поэтому число решений уравнения равно числу наборов из r + n – 1 нулей и единиц, каждый из которых имеет ровно r единиц, а это число равно .

Пример 11. E= {1, 2, 3}. Сколько сочетаний с повторениями из E по 2?

Решение: D²₃ = C²₄ = (4!)/(2!2!) = (3•4)/2 = 6. Всего таких сочетаний 6, а именно: 11, 12, 22, 23, 13, 33.

Задача. Если дано (x+y+z)⁴, как найти коэффициент при x²yz?

Решение: (x+y+z) (x+y+z) (x+y+z) (x+y+z) – из каждой скобки вытаскиваются различные переменные, таких вариантов 3⁴.

Как получается x²yz: x x y z

x y x z.

… … … …

Как подсчитать, сколько раз встретится x²yz.

Сначала мы выбираем x по максимальной степени, что будет наборов. Тогда вариантов будет для выбора y. По правилу произведения вариантов будет для выбора x²y. Аналогично, •С¹₂• С¹₁ вариантов будет для выбора x²yz. Другими словами, x²yz встретится •С¹₂•С¹₁ = •С¹₂ = (4!)/(2!2!)•(2!)(1!1!)=3•4=12 раз.

Решение подобных задач дает следующая полиномиальная

Теорема 1. .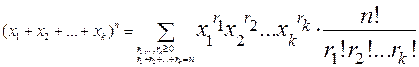

Доказательство: (x₁ + x₂ +…+ x_k)…(x₁ + x₂ +…+ x_k) – всего n скобок.

Для того чтобы выбрать r₁ штук x₁ из n скобок необходимо вариантов. Далее у нас осталось (n – r₁) скобок, значит, число выборов r₂ штук x₂ из (n – r₁) скобок будет . Тогда общее число выборов будет и т.д. Тогда число выборов r_k штук x_k из (n – r₁ –…– r_k-1) скобок будет , так как r₁ +…+ r_k = n.

Всего выборов будет

n!

=

r ₁! r ₂!... r_k!

Значит, коэффициент при будет .

Пример 12. Найти коэффициент при x²yz в (x+y+z)⁴.

Решение: По полиномиальной теореме коэффициент при x²yz будет равен (4!)/(2! ·1! ·1!)=3·4=12.

Пример 13. Сколько различных сочетаний букв можно составить из слова МАКАКА.

Решение: Используем полиномиальную теорему. Будем оперировать с буквами как с выражениями вида (М+А+К)⁶.

Так как в слове МАКАКА букв →

то число искомых слов (различных сочетаний букв из слова МАКАКА) будет равно коэффициенту при члене

МА³К² → = 60.