Формулы

Пусть имеется некоторое подмножество B P _2.

Определение. Формулой над множеством называется выражение вида:

1) , если ;

2) , если , а – либо формула над , либо переменная из нашего алфавита, где .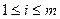

При этом никаких других формул над нет.

Пример: Пусть . Рассмотрим следующее выражение: , которое является формулой над , так как:

1. – формулы по определению.

2. 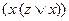– вместо подставляем – значит, формула.

3. – тоже формула.

Формулы удобно обозначать с помощью деревьев:

3.3. Сопоставление формулам над множеством
функций

Определение. 1) Если формула есть выражение вида , где , то формуле соответствует функция .

2) Если формула есть выражение вида , где ,

а) – формула над 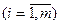, то выражению сопоставлена функция ;

б) – переменная 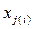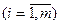, то сопоставлена тождественная функция .

Тогда формуле вида сопоставим функцию .

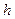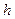Определение. Если формуле сопоставлена функция , то говорят, что формула реализует функцию . Тогда функцию 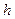называют суперпозицией функций из множества , а процесс получения функции 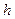из функций множества будем называть операцией суперпозиции.

Определение. Формулы и G называются эквивалентными (Ф~G), если они реализуют одинаковые функции.

Пример: Пусть .

Тогда Ф = (((x ₁ x ₂)+ x ₁)+ x ₂) является формулой над , она строится за три шага. Мы имеем следующие подформулы , , .

Формуле соответствует функция 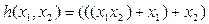, она определяется следующим образом:

0 0 0 1 1 0 1 1

Очевидно, что .

Пример: Пусть даны формулы Ф=(x→y), G=(). Ф~G?

x y
0 0 0 1 1 0 1 1

Формулы и G эквивалентны, так как реализуют одинаковые функции.