Решение уравнения (∗) в целых числах

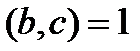Заметим, что из теоремы 11.1 легко следует, что для любых целых чисел верны следующие утверждения. 1) Если ⋮ , то ⋮ . 2) Если , и , то 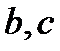- полные квадраты, т.е. такие числа, для которых существуют целые числа : .

Далее, если и - целые решения уравнения (∗), то ⋮ . Поэтому достаточно рассмотреть только случай .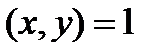

Более того, числа 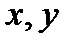не могут быть оба нечётными. Действительно, если , где , то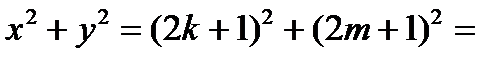

Но тогда правая часть равенства, а значит, и левая, делится на 2, но не делится на 4. В этом случае сумма не может быть полным квадратом.

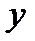Рассмотрим случай, когда - чётное целое число, - нечётное (второй случай аналогичен рассматриваемому). Тогда - нечётное число и , где оба множителя справа являются нечётными целыми числами. Пусть . Тогда , где - взаимно простые нечётные целые числа и, выражая из предыдущих равенств, получим: . Кроме того, , а значит, ⋮ , ⋮ , что по условиям выше влечёт равенство . Поэтому . 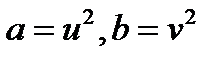Но тогда - полные квадраты, , где по предыдущему - нечётные взаимно простые целые числа. Таким образом, все определяющие (взаимно простые) целые решения уравнения 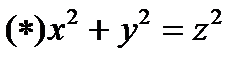имеют вид: , где – нечётные взаимно простые целые числа.