Методы Рунге-Кутта

На его основе могут быть построены разностные схемы разного порядка точности. Идея его реализации стоит в подгонке ряда Тейлора при разложении искомой функции y = y (x) в окрестностях узлов сетки в плане повышения точности этого разложения, а именно, увеличение числа производных высшего порядка без их непосредственного определения из-за сложности аналитических выражений полных производных по x от функции f (x, y).

Рассмотрим наиболее широко применяемую на практике разностную схему четвертого порядка.

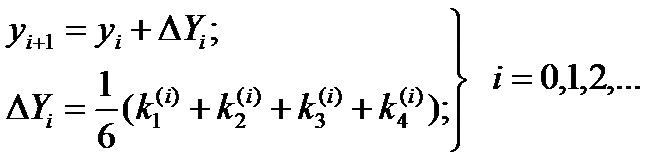Ее алгоритм состоит в следующем:

(22)

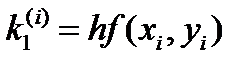
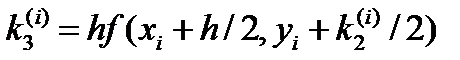
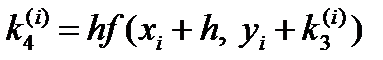
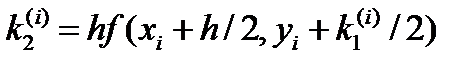
Где

В данной расчетной схеме Рунге-Кутта на каждом шаге вычисления y_i нужно 4-е раза обратиться к правой части уравнения f (x, y), т.е. метод Рунге-Кутта (22) требует бóльшего объема вычислений, однако это окупается повышенной точностью, что позволяет проводить расчет с большим шагом.

Можно показать, что метод Эйлера и его модифицирован-ный вариант является аналогом метода Рунге-Кутта первого и второго порядка, однако для достижения одинаковой точности у них шаг расчета будет значительно меньше.

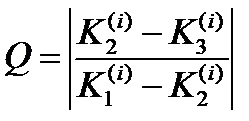Для данного метода шаг расчета можно менять при переходе от одной точке к другой. Для контроля правильности выбора шага h рекомендуется вычислять дробь

Величина Q не должна превышать нескольких сотых. В противном случае h следует уменьшать.

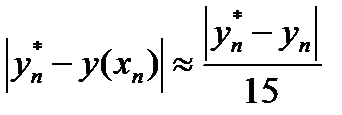Оценка погрешности метода затруднительна. Чаще всего используется грубая оценка погрешности по формуле

где y (x_n) – значение точного решения уравнения (4) в точке

x_n, а y, y_n – приближенное решение, полученное с шагом

h /2 и h.

При реализации (на ЭВМ) метода Рунге-Кутта с автоматическим выбором шага, обычно в каждой точке x _i и делают двойной просчет сначала с шагом h, потом с h /2. Если полученное y _i при этом различается в пределах допустимой точности, то шаг h для следующей точки x _i+1 удваивают, в противном случае берут половинный шаг.

В заключении следует отметить, что одношаговые методы Рунге-Кутта успешно могут быть применены к решению систем ДУ первого порядка.