Задача Коши для обыкновенных дифференциальных уравнений

В зависимости от вида ДУ (1) задача Коши формируется следующим образом.

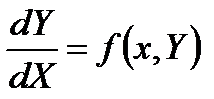1.Если n = 1, то требуется найти Y = Y (x),

удовлетворяющую уравнению: (4)

и принимающую при x = x ₀ заданное значение Y ₀: Y (x ₀) = Y ₀ (5)

Для определенности будем считать, что решение нужно получить для значений x > x ₀. В качестве начального значения может быть произвольное x, но чаще всего принимают x ₀ = 0, что не влияет на разработку численного метода для (4). Заметим, что все численные методы разработаны для решения ОДУ именно первого порядка.

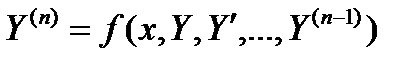2. Задача Коши для ОДУ n -го порядка

(6)

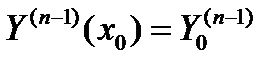
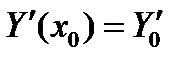
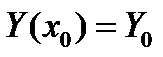найти Y = Y (x), удовлетворяющую (6) и начальным условиям

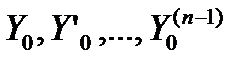(7)

Где – есть заданные числа.

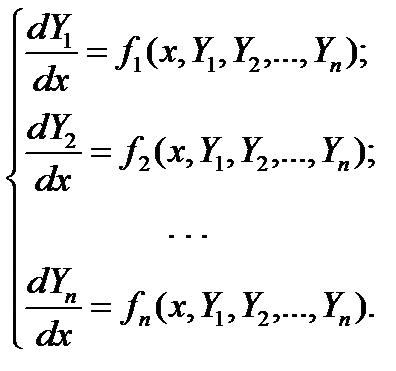3. Задача Коши для системы ДУ:

(8)

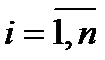
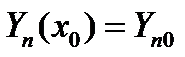
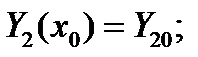
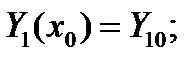Задача Коши для системы (8) заключается в отыскании Y _i(x) () удовлетворяющих (8) и начальным условиям: … (9)

Численные методы для решения ОДУ (4) и (5) применяются и для решения (8) и (9).

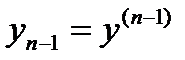
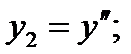
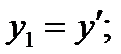Дифференциальное уравнение n -го порядка (6) может быть приведено к системе (8) путем введения новых неизвестных функций Y _i(x),

…; (10)

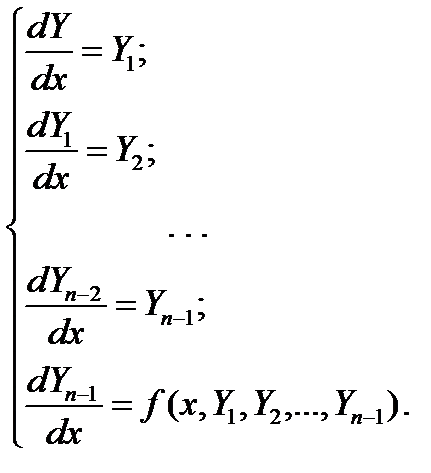Тогда (6) запишется следующим образом

Если удается найти общее решение для (4), (6), или системы (8), то задача Коши сводится к отысканию значений произвольных постоянных. Как правило, она решается приближенно