Метод Эйлера

Этот метод основан на разложении искомой функции Y (x) в ряд Тейлора в окрестностях узлов системы x = x_i (i = 0, 1, 2, …, n), в котором отбрасываются все члены, содержащие производные второго и более высоких порядков. Как правило, используется равномерная сетка D x = x_{i +1} – x_i = h = const (i =) Разложение запишем в виде

(13)

Заменяя значение функции Y (x) в узлах сетки x_i значениями сеточной функции и используя уравнение (4), получим

Тогда из (13) получим

(14)

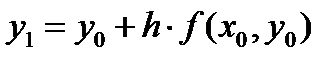При i = 0, для узла x = x ₁:

Далее по алгоритму (14)

Геометрическая интерпретация имеет вид:

На рисунке линия «0» – точное решение, линии «1» и «2» – приближенные решения.

Искомая интегральная кривая y (x), проходящая через точку (x ₀, y ₀), заменяется ломаной с вершинами в точках (x _i, y _i). Каждое звено ломаной имеет направление, совпадающее с направлением интегральной кривой (4), которая проходит через точку (x _i, y _i).

Блок-схема алгоритма будет иметь следующий вид:

Вывод полученных результатов

выполняется на каждом шаге,

но если необходимо сохранить

результаты, то следует ввести

массив значений y ₀, y ₁,..., y_n.

Локальная погрешность метода Эйлера, как видно из (13), оценивается, как О (h ²). Весь интервал [ a, b ] разбивается на n частей, тогда общая погрешность

n×О (h ²) = 1/ h × О (h ²) = О (h) – 1-й порядок.

Для оценки погрешности при машинном расчете пользуются двойным просчетом, т.е. на отрезке [ x _i, x _i+1] расчет повторяют с шагом h /2 и погрешность более точного решения у * _{i +1} (при шаге h_i /2) оценивается как разность