Метод Эйлера с пересчетом

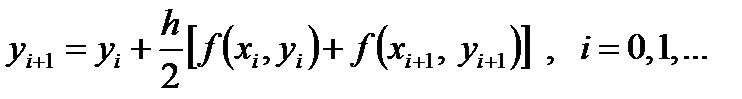При данном подходе рекуррентное соотношение (14) видоизменяется, а именно, вместо f (x _i, y _i) берут среднее арифметическое между f (x _i, y _i) и f (x_{i +1}, y_{i +1}).

Тогда (15)

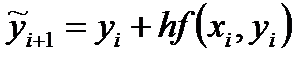Это неявная схема. Она реализуется в две итерации: сначала находится первое приближение по (14), считая y_i начальной

(16)

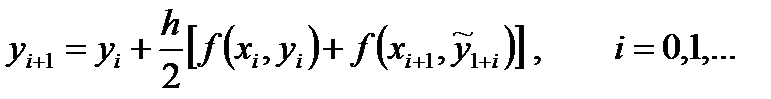затем (16) подставляется в правую часть (15) вместо y_{i +1}

(17)

Геометрическая интерпретация метода:

С помощью метода Эйлера с пересчетом можно производить контроль точности, сравнивая y_{i +1} и ỹ_{i +1}.

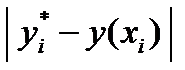
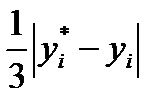На основании этого можно выбирать шаг. Если величина | ỹ_{i +1} – y_{i +1}| сравнима с заданной точностью e, то шаг можно увеличивать, если больше, то уменьшать, т.е. имеет место схема двойного просчета с оценкой погрешности по величине

≈

где y (x_i) – точное решение в точке х = x_i, а y_i и y*_i приближенные значения, полученные с шагом h и h /2, соответственно.

Метод Эйлера с последующей итерационной обработкой

Метод Эйлера можно еще более уточнить, применяя итера-ционную обработку каждого полученного значения y_i.

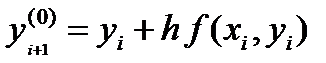А именно, сначала исходя из первого грубого приближения по (16)

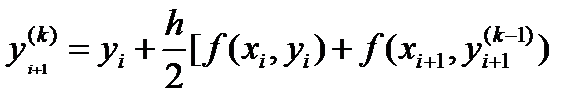строят итерационный процесс согласно (15) по следующей схеме

, k =1,2, … (18)

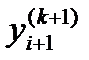
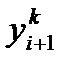Итерации продолжают до тех пор, пока в двух

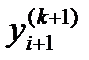последовательных приближениях, не совпадут соответствующие десятичные знаки и полагают y_{i +1}» Как правило, при достаточно малом шаге h, итерации сходятся быстро. Если после трех-четырех итераций не произошло совпадение нужного числа десятичных знаков, то шаг расчетов h уменьшается. После такой обработки значения y_i переходят к следующему узлу x_{i +1}.