Метод простої ітерації для рівняння з однією змінною

Нехай 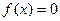(1), де 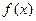неперервна на [a,b] функція. Замінимо рівняння (1) рівносильним рівнянням (2). Виберемо грубо початкове наближення і побудуємо послідовність: (3).

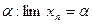Якщо послідовність збігається до числа , то перейшовши в (3) отримаємо: є розв’язком (2), а отже (1).

Виникають деякі запитання:

1) Які умови повинна задовольняти функція f(x), щоб послідовність (3) була збіжна

2) Як з(1) отримати (2), щоб функція 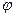забезпечувала збіжність послідовності (3)

Розглянемо графічно процес побудови ітерації:

Теорема: нехай 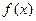задовольняє наступним умовам:

1. 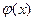визначена на [a,b]

2. 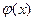неперервна на [a,b]

3.

4. (4),

тоді

1. процес ітерації збіжний при довільному значенні [a,b]
2. - єдиний розв’язок рівняння (2)
3. справедлива оцінка: (5)