 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Доведення. Щоб скористатися принципом стискуючого відображення досить показати, що в деякому околі R кореня похідна функції
|
|
Щоб скористатися принципом стискуючого відображення досить показати, що в деякому околі R кореня 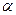 похідна функції
похідна функції  , задовільняє умову
, задовільняє умову  .
. 
Підставимо  :
:  . Запишемо для f(x) формулу Тейлора і обмежимося 3-ма доданками, тобі:
. Запишемо для f(x) формулу Тейлора і обмежимося 3-ма доданками, тобі:  . Підставивши в останню рівність x=c, отримаємо:
. Підставивши в останню рівність x=c, отримаємо: 
 , оскільки при
, оскільки при  :
:  то можна виділити такий окіл R:
то можна виділити такий окіл R: 
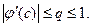
§5
МЕТОД ДОТИЧНИХ (МЕТОД НЬЮТОНА)
Розглянемо геометричну інтерпритацію даного методу. Нехай маємо рівняння 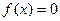 (1) і всі умови попереднього § виконуються. Беремо точку B, проводимо в ній дотичну.
(1) і всі умови попереднього § виконуються. Беремо точку B, проводимо в ній дотичну.
 |
Рівняння дотичної в точці 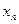 має вигляд
має вигляд  , знайдемо точку
, знайдемо точку  :
:
 (2)
(2)
Зауваження: в якості вихідної точки  слід вибирати той кінець відрізка [a,b] в якому функція має той самий знак, що і її друга похідна.
слід вибирати той кінець відрізка [a,b] в якому функція має той самий знак, що і її друга похідна.
У випадку зображеному на малюнку послідовність 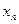 монотонно спадає і обмежена знизу, а отже вона збіжна, тобто
монотонно спадає і обмежена знизу, а отже вона збіжна, тобто  . Перейшовши до границі в рівності (2) отримаємо:
. Перейшовши до границі в рівності (2) отримаємо: 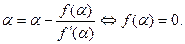 В загальному випадку справедлива така теорема.
В загальному випадку справедлива така теорема.
Відповідь про збіжність дає наступна теорема:
Теорема: нехай на відрізок [a,b] функція f(x) неперервна разом з своїми похідними другого порядку включно, які зберігають знак і не перетворюються в нуль і крім того f(a)f(b)<0. Тоді існує деякий окіл розв’язку 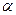 рівняння (1) що
рівняння (1) що  з цього околу послідовність
з цього околу послідовність 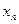 обчислена за формулою (2) збігається до кореня
обчислена за формулою (2) збігається до кореня 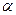 .
.
Дата публикования: 2014-11-18; Прочитано: 331 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
