 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уточнення коренів рівняння методом хорд
|
|
(МЕТОД ПРОПОРЦІЙНИХ ВІДРІЗКІВ)
Нехай дано рівняння 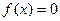 . Залишимо в силі припущення попереднього параграфа. Розглянемо геометричну ітерацію методом хорд.
. Залишимо в силі припущення попереднього параграфа. Розглянемо геометричну ітерацію методом хорд.







Мал.1 Мал.2
Виведемо рекурентну формулу для побудови наближення:



...
 (2)
(2)
Доведемо збіжність даного процесу: послідовність 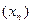 монотонно зростає і обмежена зверху, тому
монотонно зростає і обмежена зверху, тому 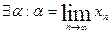 , в рівнянні (2) перейдемо до границі:
, в рівнянні (2) перейдемо до границі: 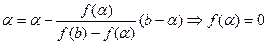
Зауваження: в загальному випадку за нерухому точку вибирають той кінець відрізка [a,b] в якому знак функції f співпадає з знаком другої похідної, тоді (2) буде:
 , (3)
, (3)

Другий кінець проміжка зручно вибирати за початкове наближення.
Виведемо формулу для оцінки точності. Нехай похідна  неперервна на [a,b], тоді вона приймає найбільше і найменше значення, тобто
неперервна на [a,b], тоді вона приймає найбільше і найменше значення, тобто  ,
,  ,
,  =0, де
=0, де 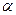 - розв’язок рівняння. Застосуємо теорему Лагранжа:
- розв’язок рівняння. Застосуємо теорему Лагранжа:  . Розкривши душки додавши до обох частин рівності вираз
. Розкривши душки додавши до обох частин рівності вираз  і звівши подібні доданки, отримаємо:
і звівши подібні доданки, отримаємо:  . Врахувавши межі зміни похідної
. Врахувавши межі зміни похідної  (4)
(4)  (5).
(5).
Виникає питання про можливість використання оцінки (5), коли мінімум похідної =0.
Відповідь про збіжність послідовності отриманої за рекурентною формулою (3) дає наступну теорему:
Теорема: нехай на відрізку [a,b] функція f(x) неперервна разом зі своїми похідними до 2-го порядку включно, причому  . Нехай також похідні
. Нехай також похідні  зберігають на [a,b] сталі знаки, тобі існує такий окіл кореня
зберігають на [a,b] сталі знаки, тобі існує такий окіл кореня 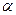 , що для
, що для  початкового наближення
початкового наближення  з цього околу послідовність (
з цього околу послідовність (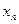 ), яка обчислюється за формулою (3), збігається до
), яка обчислюється за формулою (3), збігається до 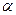 .
.
Дата публикования: 2014-11-18; Прочитано: 351 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
