Відокремлення коренів рівняння з однією змінною

Нехай задано рівняння 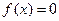(1), де 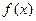визначена і неперервна на деякому скінченному чи нескінченному інтервалі.

Означення: корінь 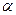рівняння (1) називається відокремленим, якщо існує деякий окіл точки 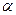в якому не має інших коренів.(для кожного рівняння вказати проміжок, що містить лише один розв’язок)

Задача знаходження наближеного розв’язку рівняння (1) поділяється на два етапи:

1. Відокремлення коренів – виділення якомога вужчих інтервалів в кожному з яких є лише один корінь.
2. Уточнення кореня – зведення його до необмеженого ступеня тосності.

Для відокремлення коренів корисними є твердження:

1. Якщо неперервна функція 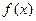на кінцях 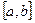приймає значення різних знаків, тобто 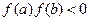, то на 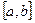є принаймі один нуль цієї функції. Якщо похідна зберігає знак, то такий нуль єдиний.

2. 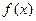є многочлен степеня m, то рівняння (1) не може мати більше ніж m коренів.

Наприклад: Відокремити корені рівняння

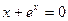
Визначити кількість коренів 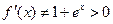зростає на всій числовій осі. Оскільки 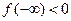. 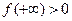, то корінь единий. Запишемо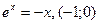

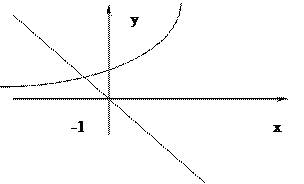
§3