 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ітераційні методи розв’язування рівнянь. Принцип стискуючих відображень в метричному просторі
|
|
Нехай дано рівняння 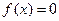 (1). Суть полягає в наступному: нехай в деякій достатньо малій області Д існує єдиний розв’язок
(1). Суть полягає в наступному: нехай в деякій достатньо малій області Д існує єдиний розв’язок 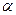 рівняння (1). Вибираємо в цій області деяку точку
рівняння (1). Вибираємо в цій області деяку точку 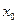 (початкове наближення) достатньо близько до
(початкове наближення) достатньо близько до 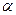 і за допомогою співвідношення
і за допомогою співвідношення 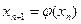 (2) будуємо послідовність точок
(2) будуємо послідовність точок 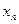 :
: 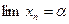 (при
(при 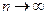 ). Вибираючи різними способами функцію
). Вибираючи різними способами функцію 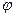 будемо отримувати різні ітераційні методи.
будемо отримувати різні ітераційні методи.
Означення: метричним простором прийнято називати впорядковану пару 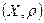 , Х - множина елементів довільної природи,
, Х - множина елементів довільної природи, 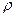 - функція відстані, яка задовольняє наступним аксіомам:
- функція відстані, яка задовольняє наступним аксіомам:
-
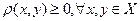 , причому
, причому 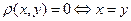
-
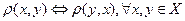
-
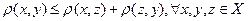
Означення: Послідовність точок  називається фундаментальною, якщо
називається фундаментальною, якщо 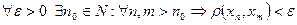
Означення: метричний простір називається повним, якщо фундаментальна послідовність є збіжна.
Означення: деякий оператор Аздійснює стискування метричного простору в себе, якщо 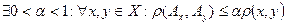
Означення: точка x називається нерухомою точкою оператора А, якщо Ax=х
Теорема1: в повному метричному просторі Х задано оператор стиску А, тоді шснує єдина нерухома точка цього відображення, тобто рівняння 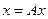 має єдиний розв’язок, який може бути знайдений як границя послідовності
має єдиний розв’язок, який може бути знайдений як границя послідовності 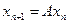 .
.
Теорема2: нехай в повному метричному просторі Х або на його частині яка містить окіл S деякої точки 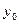 , заданий параметр А. Нехай
, заданий параметр А. Нехай 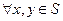 виконуються умови:
виконуються умови:
1. 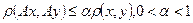
2. 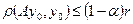
тоді в околі S існує єдиний розв’язок рівняння (3), який може бути отриманий як границя послідовності (4).
Означення: кажуть, що функція 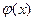 на області Д задовольняє умову Лібшеця, якщо існує деяка стала К така, що
на області Д задовольняє умову Лібшеця, якщо існує деяка стала К така, що 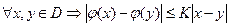 .
.
Теорема3: нехай рівняння 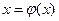 має корінь
має корінь 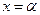 в деякому крузі S:
в деякому крузі S: 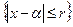 і функція
і функція 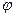 в цьому крузі задовольняє умову Лібшеця з константою К<1, тоді яке б не було
в цьому крузі задовольняє умову Лібшеця з константою К<1, тоді яке б не було  послідовність
послідовність 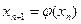 (2)
(2)
буде збігатися до 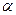 причому швидкість збіжності характеризується нерівністю
причому швидкість збіжності характеризується нерівністю
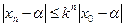 (5).
(5).
Означення: умова Лібшеця з константою к<1, буде виконуватись якщо в околі точки 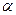 має місце нерівність
має місце нерівність
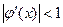 , тоді умову (5) часто записують так
, тоді умову (5) часто записують так
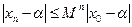 , (6)
, (6) 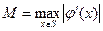 .
.
§2
Дата публикования: 2014-11-18; Прочитано: 593 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
