Доведення. Нехай дано точні числа х1,х2,,хn та Х1,Х2,,ХN

Нехай дано точні числа х1,х2,...,хn та Х1,Х2,...,ХN. Розглянемо їх алгебраїчну суму:

тоді гранична абсолютна похибка:

Наслідок: гранична абсолютна похибка суми не може бути меншою за граничну абсолютну похибку найменш точного доданку, тому існує практичне правило додавання наближених чисел з різною абсолютною точністю.

Щоб додати кілька наближених чисел з різною абсолютною точністю потрібно виділити і залишити без зміни числа, десятковий запис яких закінчується найраніше. Всі інші числа заокруглити на зразок виділених залишивши в резерві 1-2 цифри виконати додавання, отриманий результат заокруглити на 1-н знак.

Теорема: якщо доданки одного знаку, то гранична відносна похибка їх суми не перевищує найбільшої відносної похибки доданків.

Зауваження: про втрату точності при відніманні близьких чисел.

Нехай маємо два числа х1, х2. розглянемо їх різницю , , тому в обчисленнях намагаються уникати випадків, де віднімаються близькі числа.

Приклад 1.

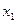=47,132

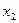=47,111

= =0,0005

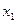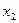= - =0,021

=0,001

=

Приклад 2:

Теорема 3: відносні похибки добутку кількох наближених чисел відмінних від нуля не перевищує суми відносних похибок цих чисел.