 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод главных элементов для решения системы уравнений
|
|

a11x1 + a12x2 + a13x3 = a14
a21x1 + a22x2 + a23x3 = a24
a31x1 + a32x2 + a33x3 = a34
На каждом этапе исключения неизвестного выбирают главный элемент ---
Наибольший по модулю коэффициент при неизвестных, затем находят
значения mi, равные частному от деления элементов столбца, содержащих главный элемент, на главный элемент, взятый с противоположным знаком.
Для получения элементов следующего этапа прибавляют главную строку (строку, содержащую главный элемент) к остальным строкам, умножая её на соответствующее значение mi.
Один из возможных вариантов схемы главных элементов приводится ниже.
| mi | Коэффициенты при неизвестных | Коэффициенты при неизвестных | Контрольные суммы S | ||
| x1 | x2 | x3 | |||
| m1 -1 m3 | a11 a21 a31 | a12 a22 a32 | a13 a23 a33 | a14 a24 a34 | a15 a25 a35 |
| -1 m3 | a’11 a’31 | a’12 a’32 | -- -- | a’14 a’34 | a’15 a’35 |
| -- | a”32 | -- | a”34 | a”35 | |
| x1 | x2 | x3 | |||
| X1 | X2 | X3 |
В приведенной схеме Ia23I=maxIaijI, Ia’11I=maxIa’ijI.
Вычисления производят по формулам: m1=-a13/a23, m3=-a33/a23;
a’1j= a1j+m1a2j (j = 1,2,4,5); a’3j= a3j+m3a2j (j = 1,2,4,5); m’3=-a’31/a’11; a”3j= a’3j+m’3a’1j (j = 2,4,5);
Неизвестные находят из соотношений:
x2= a”34/a”32; X2= a”35/a”32;
x1=(a’14– a’12x2)/a’11; X1= (a’15– a’12X2)/a’11;
x3=(a24- a21x1-a22x2)/a23; X3= (a25- a21X1-a22x2)/a23;
Контроль вычислений осуществляют так же, как и в схеме единственного деления.
Задание: решить систему уравнений с точностью до 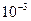 .
.
1.  16.
16. 
2.  17.
17. 
3.  18.
18. 
4.  19.
19. 
5. 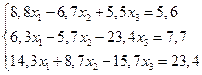 20.
20. 
6.  21.
21. 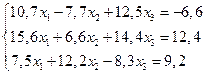
7.  22.
22. 
8. 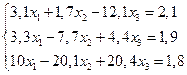 23.
23. 
9.  24.
24. 
10.  25.
25. 
11.  26.
26. 
12.  27.
27. 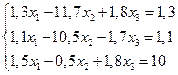
13.  28.
28. 
14.  29.
29. 
15.  30.
30. 
Лабораторная работа №8 «Метод Гаусса»
Используя схему Гаусса, решить систему уравнений с точностью до 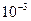 .
.
1.  16.
16. 
2. 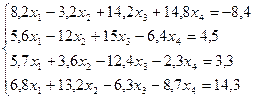 17.
17. 
3.  18.
18. 
4.  19.
19. 
5.  20.
20. 
6.  21.
21. 
7.  22.
22. 
8.  23.
23. 
9.  24.
24. 
10.  25.
25. 
11.  26.
26. 
12.  27.
27. 
13.  28.
28. 
14.  29.
29. 
15. 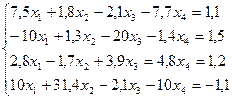 30.
30. 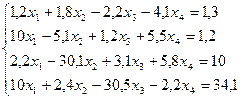
| 
| 
| 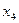
| Свободные члены |  (невязки) (невязки)
|
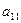
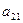
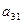
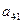
| 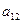
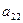
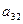
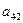
| 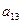
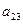
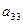
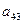
| 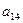
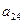
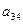
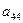
| 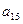
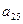
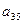
| 
|
| 
| 
| 
| 
| 
|
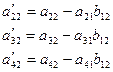
| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| |||

| 
| 
| |||

| 
|
После заполнения таблицы находим точные значения корней по формулам:

Лабораторная работа №9 «Метод Халецкого»
Решить систему уравнений по схеме Халецкого с точностью до  .
.
1.  16.
16. 
2. 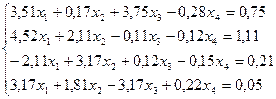 17.
17. 
3.  18.
18. 
4.  19.
19. 
5.  20.
20. 
6.  21.
21. 
7.  22.
22. 
8.  23.
23. 
9.  24.
24. 
10.  25.
25. 
11.  26.
26. 
12.  27.
27. 
13.  28.
28. 
14. 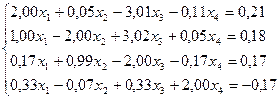 29.
29. 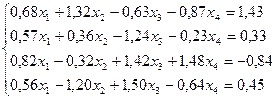
15. 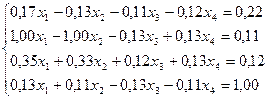 30.
30. 
Дата публикования: 2014-11-18; Прочитано: 4274 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
