 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример 1. Структура платежного баланса (по методологии МВФ) № п/п Наименование статьи I Счет текущих операций A Товары и услуги a
|
|
(справочное)
Структура платежного баланса (по методологии МВФ)
| № п/п | Наименование статьи |
| I | Счет текущих операций |
| A | Товары и услуги |
| a | Товары |
| Экспорт/импорт товаров | |
| Товары для переработки | |
| Стоимость ремонта товаров, приведения их в исправное состояние | |
| Товары, приобретаемые транспортными средствами в портах | |
| Немонетарное золото | |
| b | Услуги |
| Транспортные услуги | |
| Поездки | |
| Услуги связи | |
| Строительство | |
| Страховые услуги | |
| Финансовые услуги | |
| Услуги по экспорту/импорту информации и программного обеспечения | |
| Роялти и лицензионные платежи | |
| Прочие услуги | |
| Персональные, культурные и прочие рекреационные услуги | |
| Услуги, оказываемые правительственными учреждениями | |
| B | Доход |
| Оплата труда | |
| Доход от инвестиций | |
| 2.1 | Доход от прямых инвестиций |
| 2.2 | Доход от портфельных инвестиций |
| 2.3 | Доход от прочих инвестиций |
| C | Текущие трансферты |
| Сектор государственного управления | |
| Текущие трансферты прочих секторов | |
| 2.1 | Переводы наемных рабочих |
| 2.2 | Прочие трансферты |
| II | Счет операций с капиталом и финансовыми инструментами |
| A | Счет операций с капиталом |
| Капитальные трансферты |
Окончание табл.
| № п/п | Наименование статьи |
| 1.1 | Сектор государственного управления |
| 1.2 | Прочие капитальные трансферты |
| Приобретение/продажа непроизведенных, нефинансовых активов | |
| B | Финансовый счет |
| Прямые инвестиции | |
| 1.1 | За границу |
| 1.2 | В экономику отчетной страны |
| Портфельные инвестиции | |
| 2.1 | Активы |
| 2.2 | Обязательства |
| Прочие инвестиции | |
| 3.1 | Активы |
| 3.2 | Обязательства |
| Резервные активы | |
| 4.1 | Монетарное золото |
| 4.2 | Специальные права заимствования |
| 4.3 | Резервная позиция в МВФ |
| 4.4 | Иностранная валюта |
| 4.5 | Прочие требования |
Пример 1.
Вычислить  , где
, где 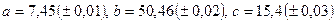 . Определить погрешность результата.
. Определить погрешность результата.
Решение.
При вычислении промежуточных результатов будем сохранять одну «запасную цифру», т.е. если по общему правилу следует оставить  значащих цифр, то в промежуточных результатах сохраним
значащих цифр, то в промежуточных результатах сохраним  цифру. Тогда:
цифру. Тогда:
1) 
При возведении приближенного числа в степень в результате следует оставить столько верных значащих цифр, сколько верных значащих цифр содержится в основании степени. Т.к. в основании степени  содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
2) 
При извлечении корня  -й степени из приближенного числа, в результате следует брать столько значащих цифр, сколько верных значащих цифр имеет подкоренное выражение. Т.к. в подкоренном выражении
-й степени из приближенного числа, в результате следует брать столько значащих цифр, сколько верных значащих цифр имеет подкоренное выражение. Т.к. в подкоренном выражении  содержится четыре верных значащих цифры, то в результате оставляем пять верных значащих цифр (одна «запасная»).
содержится четыре верных значащих цифры, то в результате оставляем пять верных значащих цифр (одна «запасная»).
3) 
Т.к. в основании степени 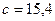 содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
4) 
В результате оставлено три значащих цифры, т.к. наименьшее число значащих цифр в числах  равно трем.
равно трем.
5) Находим предельную относительную погрешность, используя правила и определения: а) предельная относительная погрешность произведения равна сумме предельных относительных погрешностей сомножителей; б) предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя; в) предельная относительная погрешность  -й степени приближенного числа в
-й степени приближенного числа в  раз больше предельной относительной погрешности самого числа; г) предельная относительная погрешность корня
раз больше предельной относительной погрешности самого числа; г) предельная относительная погрешность корня  -й степени в
-й степени в  раз меньше предельной относительной погрешности подкоренного выражения; д)
раз меньше предельной относительной погрешности подкоренного выражения; д)  ; е)
; е) 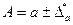 . Таким образом:
. Таким образом:

6) Находим предельную абсолютную погрешность: 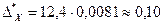
Ответ:  .
.
Пример 2. Вычислить  , где
, где  ,
,  ,
,  ,
,  ,
,  . Определить погрешность результата.
. Определить погрешность результата.
Решение.
1) 
При сложении приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. При вычислении промежуточных результатов следует сохранить на одну цифру больше. Поэтому при сложении чисел  и
и  сохраняем две цифры после запятой.
сохраняем две цифры после запятой.
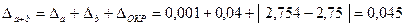
Полную погрешность находим как сумму абсолютных величин всех видов погрешностей.
2) 
При вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. При вычислении промежуточных результатов следует сохранить на одну цифру больше. Поэтому при вычитании чисел  и
и  сохраняем три цифры после запятой.
сохраняем три цифры после запятой.

Полную погрешность находим как сумму абсолютных величин всех видов погрешностей.
3) 
При возведении приближенного числа в квадрат в результате следует сохранить столько значащих цифр, сколько их в основании степени. При вычислении промежуточных результатов следует сохранить на одну цифру больше. Поэтому при вычислении  сохраняем пять значащих цифр.
сохраняем пять значащих цифр.
При умножении и делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому результат округляем до двух значащих цифр.
4) Относительная погрешность:
 .
.
5) Абсолютная погрешность:
 .
.
Ответ:  .
.
Пример 3. Пользуясь правилами подсчета цифр, вычислить  , где
, где  .
.
Решение.

 .
.
Ответ:  .
.
При вычислениях используем правила:
- При вычислениях промежуточных результатов следует сохранять на одну цифру больше, чем рекомендуют правила сложения, вычитания, умножения и деления приближенных чисел.
- При делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому
 , т.к. в числе
, т.к. в числе  три значащих цифры (+ одна «запасная» цифра).
три значащих цифры (+ одна «запасная» цифра). - При вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. Поэтому
 , т.к. наименьшее число десятичных знаков в числе 23,67 равно двум (+ одна «запасная» цифра).
, т.к. наименьшее число десятичных знаков в числе 23,67 равно двум (+ одна «запасная» цифра). - При возведении приближенного числа в квадрат в результате следует сохранить столько значащих цифр, сколько их в основании степени. Поэтому
 , т.к. в основании степени три значащих цифры (+ одна «запасная» цифра).
, т.к. в основании степени три значащих цифры (+ одна «запасная» цифра). - При умножении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому
 , т.к. в каждом числе четыре значащих цифры (+ одна «запасная» цифра).
, т.к. в каждом числе четыре значащих цифры (+ одна «запасная» цифра). - В окончательном результате «запасная» цифра отбрасывается. И т.к. меньшее число значащих цифр сомножителей равно трем (в числе 11,8), то в результате оставляем три значащих цифры.
Лабораторная работа №3 «Метод половинного деления»
- Отделить корни уравнения аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
- Отделить корни уравнения графически и уточнить один из них методом половинного деления с точностью до 0,01.
1. а)  ; б)
; б)  .
.
2. а)  ; б)
; б)  .
.
3. а)  ; б)
; б)  .
.
4. а)  ; б)
; б)  .
.
5. а)  ; б)
; б)  .
.
6. а)  ; б)
; б) 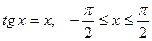 .
.
7. а)  ; б)
; б)  .
.
8. а)  ; б)
; б)  .
.
9. а)  ; б)
; б)  .
.
10. а)  ; б)
; б)  .
.
11. а)  ; б)
; б)  .
.
12. а)  ; б)
; б)  .
.
13. а)  ; б)
; б)  .
.
14. а)  ; б)
; б)  .
.
15. а)  ; б)
; б)  .
.
16. а)  ; б)
; б)  .
.
17. а)  ; б)
; б)  .
.
18. а)  ; б)
; б) 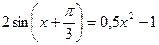 .
.
19. а)  ; б)
; б)  .
.
20. а)  ; б)
; б)  .
.
21. а)  ; б)
; б)  .
.
22. а)  ; б)
; б)  .
.
23. а)  ; б)
; б)  .
.
24. а)  ; б)
; б)  .
.
25. а)  ; б)
; б)  .
.
26. а)  ; б)
; б)  .
.
27. а)  ; б)
; б)  .
.
28. а)  ; б)
; б)  .
.
29. а)  ; б)
; б)  .
.
30. а)  ; б)
; б)  .
.
Пример 1. Отделить корни уравнения  аналитически и уточнить меньший корень уравнения методом половинного деления с точностью до
аналитически и уточнить меньший корень уравнения методом половинного деления с точностью до  .
.
Решение.
а) Отделение корней.
Обозначим  . Область определения функции
. Область определения функции 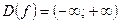 .
.
Находим производную  . Вычислим корни производной:
. Вычислим корни производной:

Составляем таблицу знаков функции  , полагая
, полагая  равным: а) критическим значениям функции (корням производной) или близким к ним; б) граничным значениям (исходя из области определения функции):
равным: а) критическим значениям функции (корням производной) или близким к ним; б) граничным значениям (исходя из области определения функции):

| 
| -2 | 
| |

| - | + | - | + |
Т.к. происходят три перемены знака функции, то уравнение имеет три действительных корня. Чтобы завершить операцию отделения корней, следует уменьшить промежутки, содержащие корни, так чтобы их длина была не больше 1. Для этого составим новую таблицу знаков функции:

| 
| -3 | -2 | -1 | 
| ||

| - | - | + | - | - | + | + |
Отсюда видно, что корни уравнения находятся в следующих промежутках:
 .
.
б) Уточняем меньший корень  , применяя метод половинного деления. Все вычисления удобно производить, используя следующую таблицу:
, применяя метод половинного деления. Все вычисления удобно производить, используя следующую таблицу:

| 
| 
| 
| 
|  
| 
| 
|
| -3 | -2 | -2,5000 | -15,6250 | 18,7500 | 0,1250 | ||
| -3 | -2,5000 | 0,5000 | -2,7500 | -20,7969 | 22,6875 | -1,1094 | |
| -2,7500 | -2,5000 | 0,2500 | -2,6250 | -18,0879 | 20,6719 | -0,4160 | |
| -2,6250 | -2,5000 | 0,1250 | -2,5625 | -16,8264 | 19,6992 | -0,1272 | |
| -2,5625 | -2,5000 | 0,0625 | -2,5313 | -16,2183 | 19,2217 | 0,0034 | |
| -2,5625 | -2,5313 | 0,0312 | -2,5469 | -16,5210 | 19,4601 | -0,0609 | |
| -2,5469 | -2,5313 | 0,0156 | -2,5391 | -16,3697 | 19,3411 | -0,0286 | |
| -2,5391 | -2,5313 | 0,0078 | -2,5352 | -16,2943 | 19,2817 | -0,0126 | |
| -2,5352 | -2,5313 | 0,0039 | -2,5333 | -16,2568 | 19,2521 | -0,0047 | |
| -2,5333 | -2,5313 | 0,0020 | -2,5323 | -16,2385 | 19,2376 | -0,0009 | |
| -2,5323 | -2,5313 | 0,0010 |
Т.к.  , то вычисления прекращаем.
, то вычисления прекращаем.
Тогда истинный корень уравнения 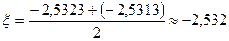 .
.
Пример 2. Отделить графически корень уравнения  . Уточнить корень методом половинного деления с точностью до
. Уточнить корень методом половинного деления с точностью до  .
.
Решение.
Запишем уравнение в виде  .
.
Построим графики функций  и
и  .
.

Из графика видно, что  .
.
Для удобства расчетов перейдем к десятичным логарифмам:
 .
.
Далее вычисления производим в таблице:

| 
| 
| 
| 
| 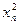
| 
| 
|
| -0,800 | -0,500 | 0,300 | -0,650 | 0,423 | -0,456 | -0,360 | |
| -0,800 | -0,650 | 0,150 | -0,725 | 0,526 | -0,561 | -0,021 | |
| -0,800 | -0,725 | 0,075 | -0,763 | 0,581 | -0,624 | 0,206 | |
| -0,763 | -0,725 | 0,038 | -0,744 | 0,554 | -0,592 | 0,088 | |
| -0,744 | -0,725 | 0,019 | -0,735 | 0,539 | -0,576 | 0,032 | |
| -0,735 | -0,725 | 0,010 |
Т.к.  , то вычисления прекращаем.
, то вычисления прекращаем.
Тогда истинный корень уравнения  .
.
Дата публикования: 2014-11-18; Прочитано: 649 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
