 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лабораторная работа №4: «Решение нелинейных уравнений методом хорд и касательных»
|
|
1) Метод хорд.
1. Отделить корни уравнения графически и уточнить один из них методом хорд с точностью до  .
.
2. Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до  .
.
1. а) 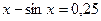 ; б)
; б)  .
.
2. а)  ; б)
; б)  .
.
3. а)  ; б)
; б) 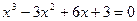 .
.
4. а)  ; б)
; б)  .
.
5. а)  ; б)
; б)  .
.
6. а)  ; б)
; б)  .
.
7. а)  ; б)
; б)  .
.
8. а)  ; б)
; б)  .
.
9. а) 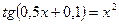 ; б)
; б)  .
.
10. а)  ; б)
; б)  .
.
11. а)  ; б)
; б)  .
.
12. а) 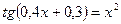 ; б)
; б)  .
.
13. а) 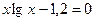 ; б)
; б)  .
.
14. а)  ; б)
; б)  .
.
15. а)  ; б)
; б)  .
.
16. а)  ; б)
; б)  .
.
17. а)  ; б)
; б)  .
.
18. а)  ; б)
; б)  .
.
19. а)  ; б)
; б) 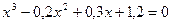 .
.
20. а)  ; б)
; б) 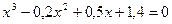 .
.
21. а)  ; б)
; б)  .
.
22. а) 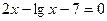 ; б)
; б)  .
.
23. а)  ; б)
; б) 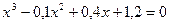 .
.
24. а)  ; б)
; б)  .
.
25. а)  ; б)
; б)  .
.
26. а)  ; б)
; б)  .
.
27. а)  ; б)
; б)  .
.
28. а)  ; б)
; б)  .
.
29. а)  ; б)
; б)  .
.
30. а)  ; б)
; б)  .
.
Образец выполнения задания.
1.Отделить корни графически уточнить один из них методом хорд до 0,001.
tg(0,55x+0,1)=x2
Обозначим у1= tg(0,55x+0,1) у2=x2
Составим таблицу значений:
| X | 0,2 | 0,4 | 0,6 | 0,8 | ||
| Y2=X2 | 0,04 | 0,16 | 0,36 | 0,64 | ||
| 0,55x+0,1 | 0,1 | 0,21 | 0,32 | 0,43 | 0,54 | 0,65 |
| Y1 | 0,100335 | 0,213142 | 0,331389 | 0,458621 | 0,59943 | 0,760204 |
Построим график:
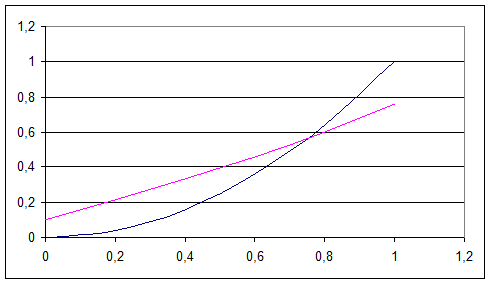
Видим, что хÎ[0,6;0,8].
Чтобы уточнить его методом хорд, определим знаки функции на концах отрезка
[0,6;0,8] и знак её второй производной в этом промежутке:
f (0,6)=tg0,43-0,36=0,0986
f (0,8)=tg0,54-0,64=-0,0406
f’ (x)=0,55/(cos2(0,55x+0,1))-2x
f’’ (x)=0,55×2cos-3(0,55x+0,1)×sin(0,55x+0,1)×0,55-2<0 при хÎ[0,6;0,8].
f’’ (x)× f (0,8)>0, значит х0=0,6
Для вычислений используем формулу:
 , где b=0,8, x0=0,6.
, где b=0,8, x0=0,6.
Вычисления производим в таблице:
| n | xn | 
|
| 0,60000 | -0,14168 | |
| 0,74168 | -0,0081 | |
| 0,74978 | -0,00039 | |
| 0,75017 | -1,9E-05 | |
| 0,75019 | -8,9E-07 |
Ответ: х»0,750.
2. Отделить корни аналитически и уточнить один из них методом хорд до 0,001.
f (x)=x3-0,2x2+0,5x+1,5
f’ (x)=3x2-0,4x+0,5 D=0,16-6<0
Составим таблицу знаков f (x):
| x | - 
| -1 | + 
| |
| Sign f(x) | - | - | + | + |
Получаем один действительный корень в промежутке [-1; 0].
Чтобы уточнить его, найдём  , в промежутке [-1; 0]
, в промежутке [-1; 0]  ,
,
f’’ (a)× f (х)>0, значит х0=b=0.
Вычисления произведём по формуле:
 ,
,
где a=-1, х0=b=0, f (a)= f (-1)-1-0,2-0,5+1,5=-0,2.
Вычисления производим в виде таблицы:
| n | xn | xn3 | xn2 | 0,2xn2 | 0,5xn | f(xn) | f(xn)+0,2 | xn-a | h |
| 1,5 | 1,7 | -0,11765 | |||||||
| -0,88235 | -0,68695 | 0,77855 | 0,15571 | -0,44118 | 0,21616 | 0,41616 | 0,11765 | -0,05654 | |
| -0,94346 | -0,83979 | 0,89012 | 0,17802 | -0,47173 | 0,01045 | 0,21045 | 0,05654 | -0,05373 | |
| -0,94627 | -0,84731 | 0,89543 | 0,17909 | -0,47313 | 0,00047 | 0,20047 | 0,05373 | -0,05361 | |
| -0,94639 |
Ответ: х»-0,946
Дата публикования: 2014-11-18; Прочитано: 3744 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
