 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные правила дифференцирования
|
|
20. 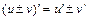 . 21.
. 21. 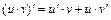 .
.
22. 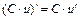 , C = const. 23.
, C = const. 23. 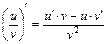 .
.
24. Дифференцирование сложной функции: пусть сложная функция y = f (j(x)) задана на интервале (a; b) и х 0 Î (a; b), тогда если внутренняя функция t = j(x) в точке х 0 имеет конечную производную 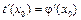 , а внешняя функция y = f (t) в точке t 0 = j(x 0) имеет конечную производную
, а внешняя функция y = f (t) в точке t 0 = j(x 0) имеет конечную производную 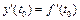 , то сложная функция y = f (j(x)) в точке х 0 имеет конечную производную, которая вычисляется по правилу:
, то сложная функция y = f (j(x)) в точке х 0 имеет конечную производную, которая вычисляется по правилу:
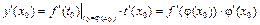 .
.
25. Дифференцирование функции, заданной параметрически: если функция задана параметрически 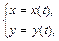 то производная вычисляется по формуле:
то производная вычисляется по формуле: 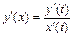 .
.
26. Дифференцирование функции, заданной неявно: если функция задана неявно уравнением 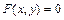 , то для нахождения ее производной дифференцируют обе части этого уравнения, считая
, то для нахождения ее производной дифференцируют обе части этого уравнения, считая 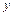 сложной функцией от
сложной функцией от 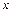 и полученное уравнение разрешают относительно
и полученное уравнение разрешают относительно 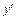 .
.
Дата публикования: 2014-11-18; Прочитано: 290 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
