 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциальное исчисление функций одной переменной. 1. Пусть функция определена на интервале (a; b)
|
|
Основные понятия
1. Пусть функция  определена на интервале (a; b). Производной функции
определена на интервале (a; b). Производной функции  в точке x 0 называется предел отношения приращения функции D f (x 0) = f (x 0 + D x) – f (x 0) в точке x 0 к приращению аргумента D x, когда
в точке x 0 называется предел отношения приращения функции D f (x 0) = f (x 0 + D x) – f (x 0) в точке x 0 к приращению аргумента D x, когда  , т. е.
, т. е.  .
.
2. Производная от функции  в точке
в точке 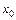 имеет геометрический смысл углового коэффициента касательной, проведенной к графику функции
имеет геометрический смысл углового коэффициента касательной, проведенной к графику функции  в точке
в точке  (рис. 2).
(рис. 2).

Рис. 2
Уравнение касательной:  .
.
Уравнение нормали:  .
.
3. Производная от пути по времени при прямолинейном движении материальной точки по закону S = S (t) имеет механический смысл мгновенной скорости в момент времени t = t 0, т. е.  .
.
4. Выражение 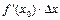 называется дифференциалом функции y = f (x) в точке x = x 0 и обозначается символом
называется дифференциалом функции y = f (x) в точке x = x 0 и обозначается символом  , где по определению обозначено dx = D x.
, где по определению обозначено dx = D x.
Дифференциал в произвольной точке х равен:  .
.
5. Дифференциал функции y = f (x) имеет геометрический смысл части приращения функции в точке х 0 при перемещении не по графику функции, а по графику касательной, проведенной в точке (х 0; f (x 0)) (рис. 2).
Таблица производных
6. 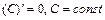 . 7.
. 7.  , a – любое.
, a – любое.
8. 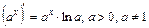 . 9.
. 9.  .
.
10.  . 11.
. 11.  .
.
12.  . 13.
. 13.  .
.
14.  . 15.
. 15.  .
.
16.  . 17.
. 17.  .
.
18. 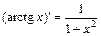 . 19.
. 19.  .
.
Дата публикования: 2014-11-18; Прочитано: 298 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
