Непрерывность функции в точке. Точки разрыва

22. Пусть функция y = f (x) определена в некоторой окрестности точки x = a и в самой точке x = a. Функция непрерывна в точке, если:

1) существует ;

2) существует f (a);

3) .

23. Точка x = a называется точкой разрыва функции y = f (x), если она принадлежит области определения функции или ее границе, но не является точкой непрерывности.

24. Если одновременно существуют предел слева и справа 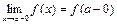и , но f (a – 0) ¹ f (a + 0), то x = a – точка разрыва первого рода.

При этом разность f (a + 0) – f (a – 0) называется скачком функции y = f (x).

25. Если существует 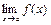, но не существует f (a), то x = a – точка устранимого разрыва.

26. Если хотя бы один из односторонних пределов 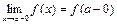или равен бесконечности, то x = a – точка разрыва второго рода.