Линейные операторы. Если указано правило, по которому вектору ставится в соответствие единственный вектор , то говорят

Если указано правило, по которому вектору ставится в соответствие единственный вектор , то говорят, что задан оператор 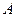, такой, что

.

Он обладает свойствами:

1. 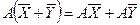– аддитивность;

2. 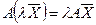– однородность,

и называется линейным оператором.

При этом вектор называют образом вектора , а сам вектор – прообразом вектора . Мы рассматриваем только случай, когда оператор 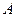задается матрицей 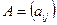, где 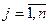_{, ,} поэтому для него справедливы свойства:

3. ;

4. ;

5. ;

6. существует нулевой оператор , такой, что ;

7. существует тождественный оператор , такой, что .

Если и , то , где . Действительно, и . Это есть свойство транзитивности линейного оператора.

Теорема 3. Матрицы и линейного оператора в базисах и связаны соотношением

,

(19)

где – матрица перехода от «старого» базиса к «новому» базису .

Доказать теорему самостоятельно.