Пример 12

Построить фундаментальную систему решений однородной системы линейных уравнений:

Решение

Выясним ранг системы, т.е. запишем матрицу

и вычислим миноры:

; ;

;

.

Следовательно, ранг системы равен 2, т.е. . А значит, система имеет ненулевые решения и, по теореме 2 фундаментальная система решений будет состоять из линейно независимых решений. При этом базисный минор и тогда однородная система равносильна системе из 2-х уравнений:

где и (при базисном миноре) являются основными (или базисными) переменными, а и – свободными, принимающими любые действительные значения.

По формуле Крамера находим и , где ,

, .

Получаем решение исходной однородной системы в виде

; , где . Полагаем для свободных переменных и и находим 2 линейно независимых решения: и .

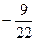
Все решения однородной системы получаются как линейная комбинация: ; – любые действительные числа.

Замечание. Геометрически полученное решение в 4-х мерном пространстве изображается 2-х мерной плоскостью, т.к. ее параметрические уравнения имеют вид:

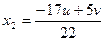, , , где .