 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример 15
|
|
Для  ,
,
т.е.  .
.
Матрица квадратичной формы в базисе из собственных векторов будет диагональной, т.е.  .
.
Действительно, составим характеристическую систему

Ее определитель равен нулю:  или
или
 , где
, где 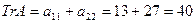 ,
,  .
.
Получим характеристическое уравнение  , корни которого
, корни которого
 ,
,  .
.
Решим систему при  :
:
 или
или 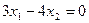 .
.
Полагаем  и получаем 1-й собственный вектор
и получаем 1-й собственный вектор  .
.
Аналогично, для  :
:
 или
или  .
.
Полагаем  и получаем 2-й собственный вектор
и получаем 2-й собственный вектор  .
.
Заметим, что  , т. к.
, т. к. 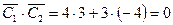 .
.
Строим матрицу перехода 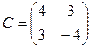 , ее определитель
, ее определитель  .
.
Обратная матрица существует:  , и в базисе из собственных векторов
, и в базисе из собственных векторов  получаем вид матрицы квадратной формы:
получаем вид матрицы квадратной формы:
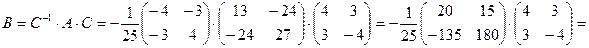
 .
.
Тогда квадратичная форма в базисе из собственных векторов примет канонический вид:
 или
или  .
.
При этом «новые»  и «старые» координаты
и «старые» координаты  связаны между собой формулой
связаны между собой формулой
 или
или 
Замечание. Аналогично для квадратичной формы от 3-х переменных
 , где , где  или или



| (24) |
.
Матрица (квадратичной формы)

| – симметрическая. |
Например,  ,
,
т. к.  .
.
В базисе из собственных векторов квадратичная форма примет вид:
 , где
, где  – собственные значения симметрической матрицы
– собственные значения симметрической матрицы  . При
. При 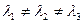 собственные векторы ортогональны.
собственные векторы ортогональны.
Замечание об евклидовых пространствах
В линейном  –мерном пространстве вводим скалярное произведение по правилу:
–мерном пространстве вводим скалярное произведение по правилу:
 . .
|
Такая операция над векторами обладает следующими свойствами:
 – коммутативность;
– коммутативность;
 – дистрибутивность;
– дистрибутивность;
 – ассоциативность по умножению на скаляр;
– ассоциативность по умножению на скаляр;
 при
при  и
и  при
при  .
.
 –мерное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, называется евклидовым пространством.
–мерное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, называется евклидовым пространством.
Длиной (нормой) вектора  в этом пространстве называется
в этом пространстве называется
 , ,
| (25) |
для которой выполняются свойства:
 , если
, если  ;
;
 при любом
при любом  ;
;
 – неравенство Коши–Буняковского;
– неравенство Коши–Буняковского;
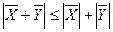 – неравенство треугольника.
– неравенство треугольника.
Угол  между векторами
между векторами  и
и  в евклидовом пространстве определяется из формулы:
в евклидовом пространстве определяется из формулы:
| (26) |
Определение корректно, т.к. согласно неравенству Коши–Буняковского
 , т. е.
, т. е.  .
.
Два вектора называется ортогональными, если  , откуда
, откуда  .
.
Векторы 
 –мерного
–мерного  пространства образуют ортонормированный базис, если
пространства образуют ортонормированный базис, если  при любых
при любых  и
и  при
при  .
.
Теорема 4. Во всяком  –мерном евклидовом пространстве существует ортонормированный базис.
–мерном евклидовом пространстве существует ортонормированный базис.
Например, в  :
:  ,
,  ,
, 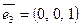 .
.
Дата публикования: 2014-11-18; Прочитано: 341 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

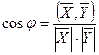 , где
, где 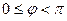 .
.