 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
G. Метод Гаусса
|
|
Для систем произвольного вида
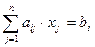 , где , где 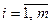
| (16) |
(прямоугольных), где число уравнений не совпадает с числом неизвестных, применяется общий метод последовательного исключения (МПИ) неизвестных, основанный на элементарных преобразованиях типа:
умножение некоторого уравнения системы на отличное от нуля число;
прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число, отличное от нуля;
перестановка местами двух уравнений системы.
Такие преобразования системы не изменяют множество ее решений и называются преобразованиями типа Гаусса. Заметим, что, выполняя преобразования 1–3 над уравнениями системы, соответствующие элементарные преобразования производятся над строками расширенной матрицы системы:
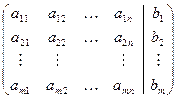 .
.
Поэтому на практике экономичней проводить МПИ в матричной форме. После конечного числа шагов элементарных преобразований приходим к матрицам вида:
| а) | 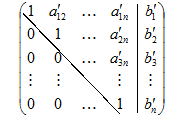
| или | б) | 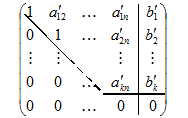
|
В случае а) система примет треугольную форму и будет иметь единственное решение, а в случае б) система примет трапециевидную форму 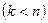 и будет иметь множество решений.
и будет иметь множество решений.
Заметим, что если на некотором шаге появится строка 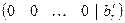 ,
, 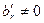 , то система будет несовместной, т.е. не будет иметь решений.
, то система будет несовместной, т.е. не будет иметь решений.
Нахождение неизвестных 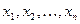 из преобразованной (треугольной или трапецевидной) системы идет снизу вверх и называется обратным ходом в методе Гаусса.
из преобразованной (треугольной или трапецевидной) системы идет снизу вверх и называется обратным ходом в методе Гаусса.
Дата публикования: 2014-11-18; Прочитано: 464 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
