 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема (о существовании и единственности разности элементов)
|
|
Для любых двух векторов  линейного пространства, существует такой единственный вектор
линейного пространства, существует такой единственный вектор 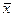 из
из 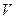 , что
, что  .
.
Доказательство. Покажем, что такой вектор существует. Возьмем  и убедимся, что этот элемент удовлетворяет уравнению
и убедимся, что этот элемент удовлетворяет уравнению  .
.
Действительно,  .
.
Докажем, что этот вектор единственный. Возьмем другой вектор  из
из 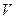 , удовлетворяющий нашему уравнению
, удовлетворяющий нашему уравнению  , и выполним следующие преобразования:
, и выполним следующие преобразования:
 .
.
Таким образом, любой вектор  , удовлетворяющий определяющему уравнению, равен
, удовлетворяющий определяющему уравнению, равен  , что и доказывает единственность такого вектора.
, что и доказывает единственность такого вектора.
Приведем еще, без подробного доказательства, несколько важных следствий из доказанной теоремы и аксиом линейного пространства.
1. Существует единственный нулевой элемент 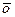 , равный
, равный  для любого
для любого 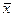 из
из 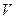 что следует из аксиом
что следует из аксиом 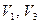 и доказанной теоремы.
и доказанной теоремы.
2. Существует единственный противоположный элемент 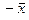 , равный
, равный  для любого
для любого 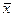 из
из 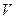 , что следует из аксиом
, что следует из аксиом  и доказанной теоремы.
и доказанной теоремы.
3. Соотношения  или
или  влекут равенство
влекут равенство  для любых
для любых  из
из 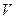 , что следует из аксиомы
, что следует из аксиомы  и доказанной теоремы.
и доказанной теоремы.
Дата публикования: 2014-11-18; Прочитано: 2821 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
