Линейное пространство

Множество 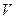элементов любой природы называется линейным или векторным пространством, а его элементы – векторами, если выполнены следующие условия.

1. Имеется операция сложения векторов, по которой каждой упорядоченной паре векторов ставится в соответствие третий вектор, что обозначается как .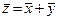

2. Имеется операция умножения числа на вектор, по которой каждой упорядоченной паре из числа и вектора ставится в соответствие вектор, что обозначается как .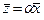

3. Для любых векторов 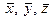из 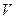и чисел 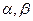указанные операции удовлетворяют следующим восьми аксиомам:

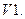Сложение коммутативно, т. е. ;

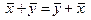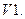Сложение ассоциативно, т. е. ;

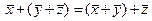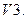Существует нулевой вектор 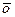такой, что для любого вектора 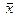выполняется ;

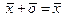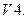Для любого вектора 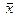существует противоположный вектор 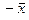такой, что выполняется ;

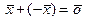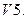Умножение вектора на число дистрибутивно относительно сложения чисел, т. е. ;

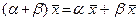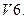Умножение вектора на число дистрибутивно относительно сложения векторов, т. е. ;

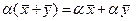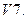Умножение на число ассоциативно, т. е. ;

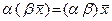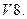При умножении на единицу вектор не изменяется, т. е. .

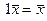Знак равенства, используемый в представленных аксиомах и во всех последующих выражениях, означает, что слева и справа от знака стоят одни и те же векторы, представленные в различных формах записи.

Подчеркнем, что, определяя линейное пространство, мы абстрагируемся как от природы изучаемых объектов, так и конкретного вида основных операций.

Таким образом, математическая структура линейной алгебры имеет вид

,

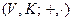причем элементы из множества 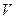называются векторами, элементы из множества 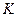являются числами (вещественными или комплексными), а операции сложения векторов и умножения числа на вектор должны удовлетворять восьми указанным выше аксиомам.

Если природа изучаемых объектов и правила выполнения двух основных операций указаны в явном виде, то соответствующее линейное пространство называют конкретным.

Рассмотрим примеры конкретных линейных пространств.