 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Множество арифметических векторов
|
|
Всякая конечная упорядоченная последовательность из 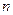 вещественных чисел называется вещественным арифметическим
вещественных чисел называется вещественным арифметическим 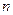 - мерным вектором и обозначается в виде
- мерным вектором и обозначается в виде 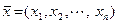 . Числа
. Числа 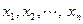 называются компонентами арифметического вектора.
называются компонентами арифметического вектора.
Сложение арифметических векторов и умножение их на число выполняется по правилам сложения соответствующих компонент и умножения каждой компоненты на число, т.е.
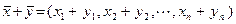 ,
, 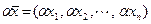 .
.
Например, если даны четырехмерные арифметические векторы  и
и 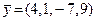 , то их сумма
, то их сумма 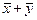 равна вектору
равна вектору 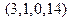 , а произведение вектора
, а произведение вектора 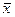 на число -2 равно вектору
на число -2 равно вектору 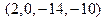 . Так как аксиомы линейного пространства выполняются для чисел, а операции
. Так как аксиомы линейного пространства выполняются для чисел, а операции 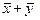 и
и 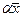 осуществляются в виде покомпонентного сложения и умножения чисел, то и для арифметических векторов любой размерности выполняются постулаты
осуществляются в виде покомпонентного сложения и умножения чисел, то и для арифметических векторов любой размерности выполняются постулаты 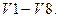 Таким образом, множество всех вещественных арифметических
Таким образом, множество всех вещественных арифметических 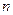 -мерных векторов с введенными выше операциями есть линейное пространство, нулевым вектором которого является вектор
-мерных векторов с введенными выше операциями есть линейное пространство, нулевым вектором которого является вектор 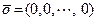 , а противоположным для каждого вектора
, а противоположным для каждого вектора 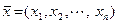 является вектор
является вектор 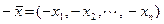 . Это пространство называют вещественным
. Это пространство называют вещественным 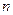 - мерным арифметическим пространством и обозначают
- мерным арифметическим пространством и обозначают 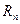 . При
. При 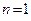 мы получаем вещественное одномерное арифметическое пространство
мы получаем вещественное одномерное арифметическое пространство 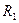 , которое совпадает со множеством вещественных чисел
, которое совпадает со множеством вещественных чисел 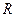 .
.
Дата публикования: 2014-11-18; Прочитано: 385 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
