Множество всех полиномов степени не выше

Элементами множества являются полиномы вида , причем старшая степень может изменяться от нуля до 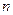. Сумма двух любых полиномов из множества и произведение любого полинома на число также принадлежат исходному множеству . Аксиомы выполняются для таких полиномов, что проверяется непосредственно. Роль нулевого полинома играет полином, у которого все коэффициенты равны нулю, а противоположным элементом для любого полинома 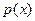служит . Множество будет вещественным или комплексным линейным пространством в зависимости от того, рассматриваем ли мы полиномы с вещественными или комплексными коэффициентами. Заметим, что множество всех полиномов степени, точно равной натуральному числу 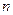, не образуют линейное пространство, так как сумма двух таких полиномов может оказаться со степенью меньшей 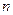, и операция суммирования выводит нас за рамки исходного множества, что недопустимо по определению линейного пространства.

Например, и полиномы второй степени, а их сумма является полиномом первой степени.

Из аксиом, определяющих линейное пространство, можно в качестве логических следствий получить ряд утверждений, справедливых для любых линейных пространств.

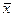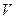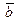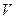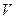Определение. Вектор , удовлетворяющий уравнению для любых из , называют разностью векторов и , и обозначают . Операцию, которая ставит в соответствие любым двум элементам из третий элемент из , называют вычитанием.

Для того, чтобы введенное определение было корректным, необходимо доказать теорему о существовании и единственности решения уравнения .