 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства билинейных форм
|
|
Любую билинейную форму можно представить в виде суммы симметричной кососимметричной форм.
При выбранном базисе e 1, e 2, …, en в векторном пространстве V любая билинейная форма A однозначно определяется матрицей
A (е) =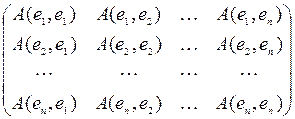 
,
так, что для любых x = x 1 e 1 + x 2 e 2 + … + xnen, y = y 1 e 1 + y 2 e 2 + … + ynen;
A (x, y) = (x 1 x 2 … xn)× ×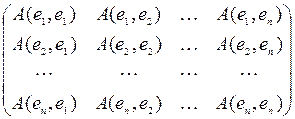 
, то есть
A (x, y) = 
, где Аij = A (ei, ej). (1)
Вид (1) назовем общим видом билинейной формы в n -мерном векторном пространстве.
Замечание. Если билинейная форма A (x, y) симметрическая, то и матрица (Aij) будет симметрической, то есть Aij = Aji для " i, j = 1, 2, …, n. Если билинейная форма A (x, y) кососимметрическая, то и матрица (Aij) будет кососимметрической, то есть Aij = – Aji для " i, j = 1, 2, …, n.
Дата публикования: 2014-11-18; Прочитано: 1873 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
