 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приведение квадратичной формы к каноническому виду
|
|
Дана квадратичная форма (2) A (x, x) =  , где x = (x 1, x 2, …, xn). Рассмотрим квадратичную форму в пространстве R 3, то есть x = (x 1, x 2, x 3), A (x, x) =
, где x = (x 1, x 2, …, xn). Рассмотрим квадратичную форму в пространстве R 3, то есть x = (x 1, x 2, x 3), A (x, x) = 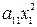 +
+ 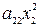 +
+ 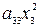 +
+ 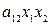 +
+ 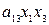 +
+ 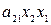 + +
+ + 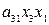 +
+ 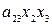 +
+ 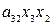 =
= 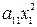 +
+ 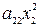 +
+ 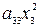 + 2
+ 2 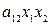 + 2
+ 2 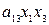 + + 2
+ + 2 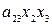 (использовали условие симметричности формы, а именно а 12 = а 21, а 13 = а 31, а 23 = а 32). Выпишем матрицу квадратичной формы A в базисе { e }, A (e) =
(использовали условие симметричности формы, а именно а 12 = а 21, а 13 = а 31, а 23 = а 32). Выпишем матрицу квадратичной формы A в базисе { e }, A (e) = 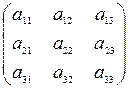 . При изменении базиса матрица квадратичной формы меняется по формуле A (f) = Ct × A (e)× C, где C – матрица перехода от базиса { e } к базису { f }, а Ct – транспонированная матрица C.
. При изменении базиса матрица квадратичной формы меняется по формуле A (f) = Ct × A (e)× C, где C – матрица перехода от базиса { e } к базису { f }, а Ct – транспонированная матрица C.
Определение 11.12. Вид квадратичной формы с диагональной матрицей называется каноническим.
Итак, пусть A (f) = 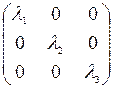 , тогда A '(x, x) =
, тогда A '(x, x) = 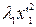 +
+ 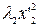 +
+ 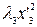 , где x '1, x '2, x '3 – координаты вектора x в новом базисе { f }.
, где x '1, x '2, x '3 – координаты вектора x в новом базисе { f }.
Определение 11.13. Пусть в n -мерном векторном пространстве V выбран такой базис f = { f 1, f 2, …, fn }, в котором квадратичная форма имеет вид
A (x, x) = 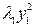 +
+ 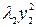 + … +
+ … + 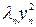 , (3)
, (3)
где y 1, y 2, …, yn – координаты вектора x в базисе { f }. Выражение (3) называется каноническим видом квадратичной формы. Коэффициенты l1, λ2, …, λ n называются каноническими; базис, в котором квадратичная форма имеет канонический вид, называется каноническим базисом.
Замечание. Если квадратичная форма A (x, x) приведена к каноническому виду, то, вообще говоря, не все коэффициенты l i отличны от нуля. Ранг квадратичной формы равен рангу ее матрицы в любом базисе.
Пусть ранг квадратичной формы A (x, x) равен r, где r ≤ n. Матрица квадратичной формы в каноническом виде имеет диагональный вид. A (f) =  , поскольку ее ранг равен r, то среди коэффициентов l i должно быть r, не равных нулю. Отсюда следует, что число отличных от нуля канонических коэффициентов равно рангу квадратичной формы.
, поскольку ее ранг равен r, то среди коэффициентов l i должно быть r, не равных нулю. Отсюда следует, что число отличных от нуля канонических коэффициентов равно рангу квадратичной формы.
Замечание. Линейным преобразованием координат называется переход от переменных x 1, x 2, …, xn к переменным y 1, y 2, …, yn, при котором старые переменные выражаются через новые переменные с некоторыми числовыми коэффициентами.
x 1 = α11 y 1 + α12 y 2 + … + α1 nyn,
x 2 = α21 y 1 + α22 y 2 + … + α2 n yn,
………………………………
x 1 = α n 1 y 1 + α n 2 y 2 + … + α nnyn.
Так как каждому преобразованию базиса отвечает невырожденное линейное преобразование координат, то вопрос о приведении квадратичной формы к каноническому виду можно решать путем выбора соответствующего невырожденного преобразования координат.
Теорема 11.2 (основная теорема о квадратичных формах). Всякая квадратичная форма A (x, x), заданная в n -мерном векторном пространстве V, с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду.
Доказательство. (Метод Лагранжа) Идея этого метода состоит в последовательном дополнении квадратного трехчлена по каждой переменной до полного квадрата. Будем считать, что A (x, x) ≠ 0 и в базисе e = { e 1, e 2, …, en } имеет вид (2):
A (x, x) =  .
.
Если A (x, x) = 0, то (aij) = 0, то есть форма уже каноническая. Формулу A (x, x) можно преобразовать так, чтобы коэффициент a 11 ≠ 0. Если a 11 = 0, то коэффициент при квадрате другой переменной отличен от нуля, тогда при помощи перенумерации переменных можно добиться, чтобы a 11 ≠ 0. Перенумерация переменных является невырожденным линейным преобразованием. Если же все коэффициенты при квадратах переменных равны нулю, то нужные преобразования получаются следующим образом. Пусть, например, a 12 ≠ 0 (A (x, x) ≠ 0, поэтому хотя бы один коэффициент aij ≠ 0). Рассмотрим преобразование
x 1 = y 1 – y 2,
x 2 = y 1 + y 2,
xi = yi, при i = 3, 4, …, n.
Это преобразование невырожденное, так как определитель его матрицы отличен от нуля 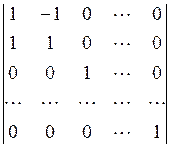 =
= 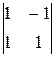 = 2 ≠ 0.
= 2 ≠ 0.
Тогда 2 a 12 x 1 x 2 = 2 a 12(y 1 – y 2)(y 1 + y 2) = 2 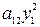 – 2
– 2 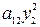 , то есть в форме A (x, x) появятся квадраты сразу двух переменных.
, то есть в форме A (x, x) появятся квадраты сразу двух переменных.
Итак, станем считать, что в равенстве (2) a 11 ≠ 0. Выделим в выражении (2) группу слагаемых, которые содержат x 1. Получим:
A (x, x) = 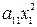 + 2
+ 2 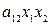 + 2
+ 2 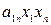 +
+ 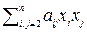 . (4)
. (4)
Преобразуем выделенную сумму к виду: 
A (x, x) = a 11 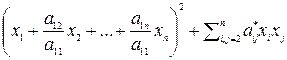 , (5)
, (5)
при этом коэффициенты aij меняются на 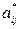 . Рассмотрим невырожденное преобразование
. Рассмотрим невырожденное преобразование
y 1 = x 1 + 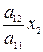 + … +
+ … + 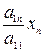 ,
,
y 2 = x 2,
………
yn = xn.
Тогда получим
A (x, x) = 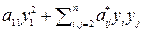 . (6).
. (6).
Если квадратичная форма 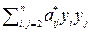 = 0, то вопрос о приведении A (x, x) к каноническому виду решен.
= 0, то вопрос о приведении A (x, x) к каноническому виду решен.
Если эта форма не равна нулю, то повторяем рассуждения, рассматривая преобразования координат y 2, …, yn и не меняя при этом координату y 1. Очевидно, что эти преобразования будут невырожденными. За конечное число шагов квадратичная форма A (x, x) будет приведена к каноническому виду (3).
Замечание 1. Нужное преобразование исходных координат x 1, x 2, …, xn можно получить путем перемножения найденных в процессе рассуждений невырожденных преобразований: [ x ] = A [ y ], [ y ] = B [ z ], [ z ] = C [ t ], тогда [ x ] = A × B ×[ z ] = A × B × C ×[ t ], то есть [ x ] = M ×[ t ], где M = A × B × C.
Замечание 2. Пусть A (x, x) = A (x, x) = 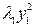 +
+ 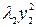 + … +
+ … + 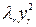 , где l i ≠ 0, i = 1, 2, …, r, причем l1 > 0, λ2 > 0, …, λ q > 0, λ q +1 < 0, …, λ r < 0.
, где l i ≠ 0, i = 1, 2, …, r, причем l1 > 0, λ2 > 0, …, λ q > 0, λ q +1 < 0, …, λ r < 0.
Рассмотрим невырожденное преобразование
y 1 = 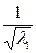 z 1, y 2 =
z 1, y 2 = 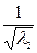 z 2, …, yq =
z 2, …, yq = 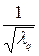 zq, yq +1 =
zq, yq +1 = 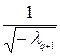 zq +1, …, yr =
zq +1, …, yr = 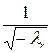 zr, yr +1 = zr +1, …, yn = zn. В результате A (x, x) примет вид:
zr, yr +1 = zr +1, …, yn = zn. В результате A (x, x) примет вид:
A (x, x) = 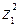 +
+ 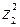 + … +
+ … + 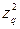 –
– 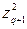 – … –
– … – 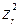 , который называется нормальным видом квадратичной формы.
, который называется нормальным видом квадратичной формы.
Пример 11.1. Привести к каноническому виду квадратичную форму A (x, x) = 2 x 1 x 2 – 6 x 2 x 3 + 2 x 3 x 1.
Решение. Поскольку a 11 = 0, используем преобразование
x 1 = y 1 – y 2,
x 2 = y 1 + y 2,
x 3 = y 3.
Это преобразование имеет матрицу A = 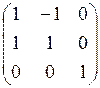 , то есть [ x ] = A [ y ] получим A (x, x) = 2(y 1 – y 2)(y 1 + y 2) – 6(y 1 + y 2) y 3 + 2 y 3(y 1 – y 2) =
, то есть [ x ] = A [ y ] получим A (x, x) = 2(y 1 – y 2)(y 1 + y 2) – 6(y 1 + y 2) y 3 + 2 y 3(y 1 – y 2) =
= 2 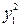 – 2
– 2 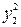 – 6 y 1 y 3 – 6 y 2 y 3 + 2 y 3 y 1 – 2 y 3 y 2= 2
– 6 y 1 y 3 – 6 y 2 y 3 + 2 y 3 y 1 – 2 y 3 y 2= 2 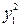 – 2
– 2 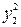 – 4 y 1 y 3 – 8 y 3 y 2.
– 4 y 1 y 3 – 8 y 3 y 2.
Поскольку коэффициент при 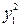 не равен нулю, можно выделить квадрат одного неизвестного, пусть это будет y 1. Выделим все члены, содержащие y 1.
не равен нулю, можно выделить квадрат одного неизвестного, пусть это будет y 1. Выделим все члены, содержащие y 1.
A (x, x) = 2(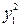 – 2 y 1 y 3) – 2
– 2 y 1 y 3) – 2 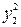 – 8 y 3 y 2 = 2(
– 8 y 3 y 2 = 2(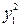 – 2 y 1 y 3 +
– 2 y 1 y 3 + 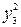 ) – 2
) – 2 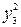 – 2
– 2 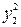 – 8 y 3 y 2 = 2(y 1 – y 3)2 – 2
– 8 y 3 y 2 = 2(y 1 – y 3)2 – 2 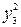 – 2
– 2 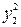 – 8 y 3 y 2.
– 8 y 3 y 2.
Выполним преобразование, матрица которого равна B.
z 1 = y 1 – y 3, Þ y 1 = z 1 + z 3,
z 2 = y 2, Þ y 2 = z 2,
z 3 = y 3; Þ y 3 = z 3.
B = 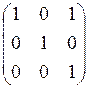 , [ y ] = B ×[ z ].
, [ y ] = B ×[ z ].
Получим A (x, x) = 2 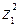 – 2
– 2 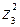 –
– 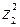 – 8 z 2 z 3. Выделим члены, содержащие z 2. Имеем A (x, x) = 2
– 8 z 2 z 3. Выделим члены, содержащие z 2. Имеем A (x, x) = 2 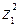 – 2(
– 2(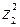 + 4 z 2 z 3) – 2
+ 4 z 2 z 3) – 2 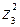 = 2
= 2 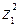 – 2(
– 2(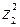 + 4 z 2 z 3 + 4
+ 4 z 2 z 3 + 4 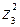 ) + + 8
) + + 8 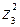 – 2
– 2 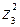 = 2
= 2 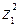 – 2(z 2 + 2 z 3)2 + 6
– 2(z 2 + 2 z 3)2 + 6 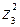 .
.
Выполняем преобразование с матрицей C:
t 1 = z 1, Þ z 1 = t 1,
t 2 = z 2 + 2 z 3, Þ z 2 = t 2 – 2 t 3,
t 3 = z 3; Þ z 3 = t 3.
C = 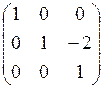 , [ z ] = C ×[ t ].
, [ z ] = C ×[ t ].
Получили: A (x, x) = 2 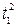 – 2
– 2 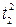 + 6
+ 6 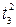 канонический вид квадратичной формы, при этом [ x ] = A [ y ], [ y ] = B [ z ], [ z ] = C [ t ], отсюда [ x ] = ABC [ t ];
канонический вид квадратичной формы, при этом [ x ] = A [ y ], [ y ] = B [ z ], [ z ] = C [ t ], отсюда [ x ] = ABC [ t ];
A × B × C = 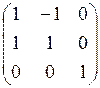 ×
× 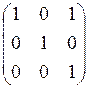 ×
× 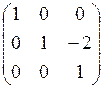 =
= 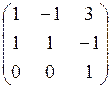 . Формулы преобразований следующие
. Формулы преобразований следующие
x 1 = t 1 – t 2 + t 3,
x 2 = t 1 + t 2 – t 3,
x 3 = t 3.
Дата публикования: 2014-11-18; Прочитано: 1238 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
