Классификация квадратичных форм

Пусть у квадратичной формы A (x, x) индекс инерции равен k, положительный индекс инерции равен p, отрицательный индекс инерции равен q, тогда k = p + q.

Было доказано, что в любом каноническом базисе f = { f ₁, f ₂, …, f_n } эта квадратичная форма A (x, x) может быть приведена к нормальному виду A (x, x) = + + … + – – 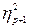… – , где h ₁, h ₂, …, h_n координаты вектора x в базисе { f }.