 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример распределения Стьюдента
|
|
Пусть имеется устройство вывода, для которого можно установить режим 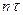
 пикселей, где
пикселей, где  - целое положительное число. Предположим, что оно получает информацию сразу по всей выходной матрице, а затем выводит ее по точкам. Тогда скорость обработки изображения будет подчиняться распределению Стьюдента.
- целое положительное число. Предположим, что оно получает информацию сразу по всей выходной матрице, а затем выводит ее по точкам. Тогда скорость обработки изображения будет подчиняться распределению Стьюдента.
Доказательство:
Так как вывод производится по точкам, то потребуется вывести точку ровно 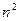 раз. Кроме того, потребуется также один раз принять информацию. В итоге получим, что требуется
раз. Кроме того, потребуется также один раз принять информацию. В итоге получим, что требуется 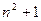 единиц времени. Скорость обработки обратно пропорциональна затраченному времени, т. е.. Если пренебречь коэффициентами, то последняя
единиц времени. Скорость обработки обратно пропорциональна затраченному времени, т. е.. Если пренебречь коэффициентами, то последняя 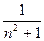 формула соответствует формуле для плотности распределения Стьюдента при
формула соответствует формуле для плотности распределения Стьюдента при  .
.
Распределение Фишера – это распределение случайной величины 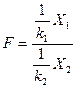 ,
,
где случайные величины 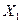 и
и 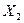 независимы и имеют распределения хи – квадрат с числом степеней свободы
независимы и имеют распределения хи – квадрат с числом степеней свободы  и
и  соответственно. При этом пара (
соответственно. При этом пара ( ,
,  ) – пара «чисел степеней свободы» распределения Фишера, а именно,
) – пара «чисел степеней свободы» распределения Фишера, а именно,  – число степеней свободы числителя, а
– число степеней свободы числителя, а  – число степеней свободы знаменателя. Распределение случайной величины
– число степеней свободы знаменателя. Распределение случайной величины 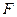 названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики.
Предположим теперь, что каждая из 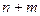 независимых случайных величин
независимых случайных величин 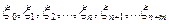 распределена нормально с параметрами
распределена нормально с параметрами  и
и 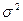 (
( ). Тогда случайная величина
). Тогда случайная величина  имеет F-распределение с
имеет F-распределение с  и
и  степенями свободы (записывается
степенями свободы (записывается 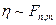 ).
).
График функции плотности 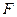 -распределения представлен на рис. 2.1.3 в двух вариантах:
-распределения представлен на рис. 2.1.3 в двух вариантах:  и
и  .
.
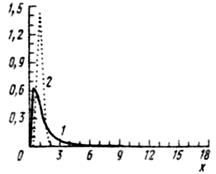
Рис. 2.1.3. Функция плотности 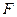 -распределения: (1)
-распределения: (1)  ; (2)
; (2)  .
.
Основные характеристики распределения Фишера
| Обозначение | 
|
| Область значений | 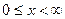
|
| Параметры | Количества степеней свободы – целые положительные числа  и и  , параметры формы. , параметры формы.
|
| Плотность |  
|
| Математическое ожидание | 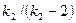 , , 
|
| Дисперсия | 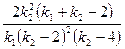 , , 
|
| Функция распределения | Не выражается в элементарных функциях |
| Мода |  , если , если 
|
| Коэффициент асимметрии | 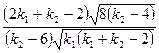 , если , если 
|
Свойства распределения:
1. Если  , то
, то 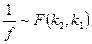
 .
.
2. Распределение Фишера сходится к единице, если  , то
, то  по распределению при
по распределению при 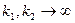 , где
, где 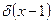 -дельта-функция в единице, т.е. распределение случайной величины-константы
-дельта-функция в единице, т.е. распределение случайной величины-константы 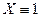 .
.

Связь с другими распределениями:
1. Если  , то случайные величины
, то случайные величины 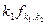 сходятся по распределению к
сходятся по распределению к 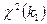 при
при 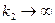 .
.
Дата публикования: 2014-11-18; Прочитано: 2432 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
