 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример. Рассмотрим пространство элементарных событий, которое получается в результате независимых бросаний двух монет
|
|
Рассмотрим пространство элементарных событий, которое получается в результате независимых бросаний двух монет. В этом примере пространство элементарных событий состоит из четырех элементарных событий, которым сопоставляется вероятность 1/4. Определим теперь на этом пространстве случайную величину  , равную числу гербов, появившихся при бросании двух монет. Очевидно, что значения случайной величины
, равную числу гербов, появившихся при бросании двух монет. Очевидно, что значения случайной величины  есть 0, 1, 2, и случайная величина принимает эти значения с вероятностями 0,25, 0,5, 0,25, соответственно.
есть 0, 1, 2, и случайная величина принимает эти значения с вероятностями 0,25, 0,5, 0,25, соответственно.
Так как одномерная случайная величина  представляет собой числовую функцию на пространстве элементарных событий, то любая числовая функция
представляет собой числовую функцию на пространстве элементарных событий, то любая числовая функция  от случайной величины в соответствии с определением также является случайной величиной.
от случайной величины в соответствии с определением также является случайной величиной.
Определение 1.1. Функцией распределения вероятностей, или просто функцией распределения (иногда применяют термин кумулятивная функция распределения) случайной величины  , называется функция
, называется функция 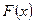 , равная для любого значения
, равная для любого значения  вероятности события
вероятности события  :
:
 (1.1)
(1.1)
Иногда в литературе применяется другое обозначение функции распределения вероятностей случайной величины  .
.
Из определения (1.1) легко вывести свойства функции распределения:
1. 
2. 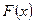 - неубывающая функция
- неубывающая функция
3. 
4. 
5.  .
.
Графическое изображение функции распределения представляет собой неубывающую кривую, значения которой лежат в интервале от 0 до 1 (рис.1.1, рис.1.2).


Рис.1.1. Распределение непрерывной Рис.1.2. Распределение дискретной
случайной величины случайной величины
На рис. 1.3 приведен график функции распределения вероятностей случайной величины из примера, рассмотренного ранее.

Рис. 1.3. Функция распределения F (x) случайной величины.
Важнейшими среди характеристик распределений являются математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации, моменты, центральные моменты, коэффициент асимметрии, коэффициент эксцесса, медиана, мода, первая квартиль, третья квартиль, интерквартильный размах, квантили.
Определение 1.2. Математическим ожиданием случайной величины  (иногда применяется термин среднее или генеральное среднее) называется число
(иногда применяется термин среднее или генеральное среднее) называется число  (другие распространенные обозначения:
(другие распространенные обозначения:  ), равное
), равное
 , если
, если  - дискретная случайная величина и
- дискретная случайная величина и
 , если
, если  - непрерывная случайная величина.
- непрерывная случайная величина.
Математическое ожидание  является характеристикой положения центра распределения, или, как иногда говорят, мерой центральной тенденции, или средним по вероятностям случайной величины.
является характеристикой положения центра распределения, или, как иногда говорят, мерой центральной тенденции, или средним по вероятностям случайной величины.
Свойства математического ожидания:
1.  , где
, где  - константа
- константа
2.  , где
, где 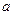 и
и  - константы
- константы
3. Для любых двух случайных величин  и
и  :
: 
4. Если  и
и  - независимые случайные величины, то
- независимые случайные величины, то 
 5. Если
5. Если  - некоторая функция, то (при довольно общих ограничениях)
- некоторая функция, то (при довольно общих ограничениях) 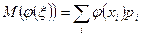 для дискретной случайной величины
для дискретной случайной величины  и
и  для непрерывной случайной величины
для непрерывной случайной величины  .
.
Для описания многих практически важных свойств случайной величины необходимо знание не только ее математического ожидания, но и отклонения возможных ее значений от среднего значения.
Для измерения разброса значений случайной величины около среднего значения часто используют такие характеристики как дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Определение 1.3. Дисперсией случайной величины называется число  (другие распространенные обозначения:
(другие распространенные обозначения:  ), равное
), равное
 если
если  - дискретная случайная величина, и
- дискретная случайная величина, и  если
если  - непрерывная случайная величина.
- непрерывная случайная величина.
Дисперсия характеризует средний квадрат отклонения случайной величины от своего математического ожидания.
Свойства дисперсии:
1. 
2. 
3.  , где
, где  - константа
- константа
4.  , где
, где 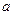 и
и  - константы
- константы
5. Если  и
и  - независимые случайные величины, то
- независимые случайные величины, то 
Из свойств  следует, что
следует, что  , причем равенство имеет место только при
, причем равенство имеет место только при  . Т.е.
. Т.е.  минимизирует средний квадрат отклонения
минимизирует средний квадрат отклонения  .
.
Определение 1.4. Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число  , равное
, равное  .
.
Среднее квадратическое отклонение, следовательно, является, как и дисперсия, мерой рассеяния распределения, но измеряется, в отличие от дисперсии, в тех же единицах, которые используют для измерения значений случайной величины.
Определение 1.5. Коэффициентом вариации случайной величины  называется число
называется число  , равное, если
, равное, если  ,
,  .
.
Таким образом, коэффициент вариации является, как и дисперсия, и среднее квадратическое отклонение, мерой рассеяния распределения, но служит для измерения среднего квадратического отклонения в долях математического ожидания.
Определение 1.6. Моментом порядка  (иногда применяют термин «начальный момент порядка
(иногда применяют термин «начальный момент порядка  ») случайной величины называется число
») случайной величины называется число  , равное
, равное  .
.
Определение 1.7 Центральным моментом порядка  случайной величины
случайной величины  называется число
называется число  , равное
, равное  .
.
Таким образом, математическое ожидание случайной величины есть момент первого порядка, а дисперсия - центральный момент второго порядка.
Кроме этих моментов наиболее часто используется третий и четвертый центральные моменты.
Определение 1.8. Коэффициентом асимметрии («скошенности») случайной величины  называется величина
называется величина  , а коэффициентом эксцесса («островершинности») случайной величины
, а коэффициентом эксцесса («островершинности») случайной величины  - величина
- величина  .
.

Рис. 1.4. Пример распределений с положительной ( ) и отрицательной (
) и отрицательной ( ) асимметрией.
) асимметрией.
Если плотность распределения случайной величины симметрична, то коэффициент асимметрии 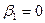 . На рис. 1.4 приведены графики функций плотности в двух случаях:
. На рис. 1.4 приведены графики функций плотности в двух случаях:  . Для нормального распределения коэффициент эксцесса
. Для нормального распределения коэффициент эксцесса 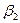 равен 3. Если же распределение сосредоточено вокруг среднего теснее, чем нормальное, то
равен 3. Если же распределение сосредоточено вокруг среднего теснее, чем нормальное, то  , в противном случае
, в противном случае 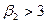 .
.
Другими характеристиками положения являются медиана и мода.
Определение 1.9. Медианой случайной величины  называется такое число
называется такое число  , что
, что 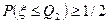 ,
, 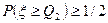 .
.
Если  - непрерывная случайная величина, то определение медианы полезно интерпретировать через функцию плотности, как это показано на рис. 1.5. Таким образом, для непрерывной случайной величины
- непрерывная случайная величина, то определение медианы полезно интерпретировать через функцию плотности, как это показано на рис. 1.5. Таким образом, для непрерывной случайной величины  .
.

Рис. 1.5. Медиана распределения
Если распределение случайной величины симметрично, как, например, в случае нормального распределения, то медиана совпадает с математическим ожиданием. Иногда математическому ожиданию приписывается смысл медианы, что, конечно же, неверно, так как математическое ожидание и медиана для несимметричных распределений, вообще говоря, не совпадают.
Определение 1.10. Модой непрерывной случайной величины называется такое значение  , в котором
, в котором  достигает своего локального максимума.
достигает своего локального максимума.

Рис. 1.6. Мода, медиана и математическое ожидание.
Мода есть «центр сгущения» случайной величины в смысле наиболее часто встречающихся значений случайной величины. Распределение с одной модой называется унимодальным, а распределение с несколькими модами - мультимодальным. Для симметричного унимодального распределения мода совпадает с математическим ожиданием, а, следовательно, и с медианой. Как в случае с медианой, иногда математическому ожиданию приписывают смысл моды, что, конечно же, неверно, так как математическое ожидание и мода для несимметричных распределений не совпадают.
На рис. 1.6 для несимметричного унимодального распределения показаны все три характеристики положения распределения.
Можно ввести еще две характеристики распределения, аналогичные медиане: первую квартиль и третью квартиль.
Определение 1.11. Первой квартилью распределения случайной величины  называется такое число
называется такое число  что
что  ,
, 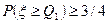 , а третьей квартилью распределения случайной величины
, а третьей квартилью распределения случайной величины  называется такое число
называется такое число  , что
, что 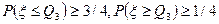 .
.
Если  - непрерывная случайная величина, то это определение квартили полезно интерпретировать через функцию плотности в соответствии с рис. 1.7.
- непрерывная случайная величина, то это определение квартили полезно интерпретировать через функцию плотности в соответствии с рис. 1.7.

Рис. 1.7. Первая и третья квартили распределения.
Таким образом, для непрерывной случайной величины 
 и
и  .
.
Следовательно, вероятность того, что случайная величина примет значение в интервале  , равна
, равна  .
.
Заметим, что длина этого интервала  называется интерквартильным размахом и может служить, аналогично среднеквадратическому отклонению, мерой рассеяния значений случайной величины.
называется интерквартильным размахом и может служить, аналогично среднеквадратическому отклонению, мерой рассеяния значений случайной величины.
Определение 1.12. Квантилью порядка  распределения
распределения  называется число
называется число  , такое, что
, такое, что  .
.
Для непрерывной случайной величины это определение полезно интерпретировать через функцию плотности, как показано на рис. 1.8.
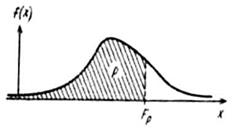
Рис. 1.8. Графическая иллюстрация определения квантили.
Из определения квантили следует, что медиана есть квантиль порядка 0.5, первая квартиль - квантиль порядка 0.25, а третья квартиль - квантиль порядка 0.75.
Для некоторых, наиболее распространенных в математической статистике распределений созданы таблицы квантилей.
Очень часто, особенно в пакетах прикладных программ по статистической обработке, вместо термина «квантиль» используется термин «процентиль», когда порядок квантили выражается в процентах.

§2. Анализ функций распределения
Дата публикования: 2014-11-18; Прочитано: 1670 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
